همانطور که میدانید، MetaTrader 5 امکان بهینه سازی استراتژیهای معاملاتی را با استفاده از استراتژی تستر داخلی بر اساس دو الگوریتم فراهم میکند: شمارش مستقیم پارامترهای ورودی و الگوریتم ژنتیک – GA. بهینه سازی ژنتیک نوعی الگوریتم تکاملی است که سرعت قابل توجه فرآیند را فراهم میکند. با این حال، نتایج GA میتواند به طور قابل توجهی به وظیفه و مشخصات یک اجرای خاص GA ، به ویژه مواردی که توسط تستر ارائه میشود، بستگی داشته باشد. به همین دلیل بسیاری از معامله گرانی که مایل به افزایش عملکرد استاندارد هستند سعی میکنند بهینه سازهای خود را برای MetaTrader ایجاد کنند. در این جا، روش های بهینه سازی سریع، محدود به الگوریتم ژنتیک نیستند. علاوه برGA ، روشهای معروف دیگری مانند الگوریتم تبرید شبیه سازی شده و بهینه سازی ازدحام ذرات نیز وجود دارد. در این مقاله، الگوریتم PSO (الگوریتم بهینه سازی ازدحام ذرات) را پیاده سازی خواهیم کرد و سعی خواهیم کرد آن را در تستر MetaTrader ادغام کنیم تا به صورت موازی بر روی عوامل محلی موجود اجرا شود. تابع بهینه سازی هدف، معیار عملکرد معامله EA است که توسط کاربر انتخاب شده است.
روش ازدحام ذرات در الگوریتم PSO
از نظر الگوریتمی ، روش الگوریتم PSO نسبتاً ساده است. ایده اصلی، تولید مجموعه ای از “ذرات” مجازی در فضای پارامترهای ورودی Expert Advisor است. سپس ذرات، بسته به معیارهای معاملات EA در نقاط مربوط به فضا حرکت کرده و سرعت خود را تغییر میدهند. این روند چندین بار تکرار میشود تا زمانی که عملکرد بهبود یابد. شبه کد الگوریتم در زیر نشان داده شده است:

طبق این کد، هر ذره دارای موقعیت فعلی، سرعت و حافظه “بهترین” نقطه خود در گذشته است. در این جا، “بهترین” نقطه به معنای نقطهای (مجموعهای از پارامترهای ورودی EA) است، که بالاترین مقدار تابع هدف برای این ذره به دست میآید. بگذارید این را در یک کلاس توصیف کنیم.
class Particle { public: double position[]; // current point double best[]; // best point known to the particle double velocity[]; // current speed double positionValue; // EA performance in current point double bestValue; // EA performance in the best point int group; Particle(const int params) { ArrayResize(position, params); ArrayResize(best, params); ArrayResize(velocity, params); bestValue = -DBL_MAX; group = -1; } };
اندازه همه آرایه ها با بعد فضای بهینه سازی برابر است، بنابراین برابر است با تعداد پارامترهای Expert Advisor بهینه سازی شده (منتقل شده به سازنده). به طور پیش فرض، هرچه مقدار تابع هدف بزرگتر باشد، بهینه سازی بهتر است. بنابراین، bestValue را با حداقل تعداد -DBL_MAX ممکن مقدار دهی کنید. یکی از معیارهای معاملات مانند سود، ضریب سود، نسبت شارپ و غیره معمولاً به عنوان معیار ارزیابی EA استفاده میشود. اگر بهینه سازی توسط پارامتری که مقادیر پایینتر آن بهتر تلقی میشود، انجام شود، مانند افت سرمایه، میتوان برای به حداکثر رساندن مقادیر مخالف، تغییرات مناسب را ایجاد کرد.
آرایه ها و متغیرها برای ساده سازی دسترسی و کد محاسبه مجدد آنها به صورت public در می آیند. رعایت دقیق اصول OOP مستلزم پنهان کردن آن ها با استفاده از اصلاح کننده “private” و توصیف روشهای خواندن و اصلاح است.
علاوه بر ذرات منفرد، الگوریتم با اصطلاحاً “توپولوژی” یا زیر مجموعه ذرات عمل میکند. با توجه به اصول مختلف می توان آنها را ایجاد کرد. “توپولوژی گروه اجتماعی” در مورد ما استفاده خواهد شد. چنین گروهی اطلاعاتی را درباره بهترین موقعیت در بین تمام ذرات خود ذخیره میکند.
class Group { private: double result; // best EA performance in the group public: double optimum[]; // best known position in the group Group(const int params) { ArrayResize(optimum, params); ArrayInitialize(optimum, 0); result = -DBL_MAX; } void assign(const double x) { result = x; } double getResult() const { return result; } bool isAssigned() { return result != -DBL_MAX; } };
با تعیین یک نام گروه در قسمت ” group از کلاس Particle، گروهی را که ذره به آن تعلق دارد نشان میدهیم (به بالا نگاه کنید).
حال، اجازه دهید ما به سراغ برنامه نویسی خود الگوریتم PSO برویم. به عنوان یک کلاس جداگانه اجرا خواهد شد. بیایید با آرایه های particles و groups شروع کنیم.
class Swarm { private: Particle *particles[]; Group *groups[]; int _size; // number of particles int _globals; // number of groups int _params; // number of parameters to optimize
برای هر پارامتر، ما باید محدوده ای از مقادیر را که در آن بهینه سازی انجام میشود، و همچنین یک افزایش مرحله ای (مرحله) را مشخص کنیم.
double highs[]; double lows[]; double steps[];
علاوه بر این، مجموعه بهینه پارامترها باید در جایی ذخیره شود.
double solution[];
از آن جا که کلاس، چندین سازنده مختلف خواهد داشت، بیایید متد مقداردهی اولیه یکنواخت را توصیف کنیم.
void init(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { _size = size; _globals = globals; _params = params; ArrayCopy(highs, max); ArrayCopy(lows, min); ArrayCopy(steps, inc); ArrayResize(solution, _params); ArrayResize(particles, _size); for(int i = 0; i < _size; i++) // loop through particles { particles[i] = new Particle(_params); ///do ///{ for(int p = 0; p < _params; p++) // loop through all dimensions { // random placement particles[i].position[p] = (MathRand() * 1.0 / 32767) * (highs[p] - lows[p]) + lows[p]; // adjust it according to step granularity if(steps[p] != 0) { particles[i].position[p] = ((int)MathRound((particles[i].position[p] - lows[p]) / steps[p])) * steps[p] + lows[p]; } // the only position is the best so far particles[i].best[p] = particles[i].position[p]; // random speed particles[i].velocity[p] = (MathRand() * 1.0 / 32767) * 2 * (highs[p] - lows[p]) - (highs[p] - lows[p]); } ///} ///while(index.add(crc64(particles[i].position)) && !IsStopped()); } ArrayResize(groups, _globals); for(int i = 0; i < _globals; i++) { groups[i] = new Group(_params); } for(int i = 0; i < _size; i++) { // random group membership particles[i].group = (_globals > 1) ? (int)MathMin(MathRand() * 1.0 / 32767 * _globals, _globals - 1) : 0; } }
همه آرایه ها با توجه به بعد داده شده توزیع میشوند و با داده های منتقل شده پر میشوند. موقعیت اولیه ذرات، سرعت آنها و عضویت در گروه به طور تصادفی تعیین میشود. نکته مهمی در کد بالا ذکر شده است. کمی بعد به این موضوع خواهیم پرداخت.
توجه داشته باشید که نسخه کلاسیک الگوریتم PSO برای بهینه سازی توابع تعریف شده روی مختصات پیوسته در نظر گرفته شده است. با این حال، پارامترهای EA معمولاً با یک مرحله مشخص تست میشوند. به عنوان مثال، یک میانگین متحرک استاندارد نمیتواند 5.11 دوره داشته باشد. به همین دلیل است که علاوه بر طیف وسیعی از مقادیر قابل قبول برای همه ابعاد، مرحله استفاده شده برای گرد کردن موقعیت ذرات را تنظیم میکنیم. این کار نه تنها در مرحله مقدماتی، بلکه در محاسبات هنگام بهینه سازی نیز انجام خواهد شد.
اکنون، ما میتوانیم چند سازنده را با استفاده از init پیاده سازی کنیم.
#define AUTO_SIZE_FACTOR 5 public: Swarm(const int params, const double &max[], const double &min[], const double &step[]) { init(params * AUTO_SIZE_FACTOR, (int)MathSqrt(params * AUTO_SIZE_FACTOR), params, max, min, step); } Swarm(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { init(size, globals, params, max, min, step); }
مورد اول برای محاسبه اندازه جمعیت و تعداد گروه ها بر اساس تعداد پارامترها از یک قانون کلی شناخته شده استفاده میکند. ثابت AUTO_SIZE_FACTOR را که به طور پیش فرض 5 است، میتوان به دلخواه تغییر داد. سازنده دوم به طور صریح مشخصات همه مقادیر را مجاز میداند.
مخرب حافظه اختصاص داده شده را آزاد میکند.
~Swarm()
{
for(int i = 0; i < _size; i++)
{
delete particles[i];
}
for(int i = 0; i < _globals; i++)
{
delete groups[i];
}
}
اکنون وقت آن است که روش اصلی کلاس را که مستقیماً بهینه سازی را انجام میدهد، بنویسیم.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4)
اولین پارامتر، Functor & f، مورد توجه خاص است. بدیهی است که Expert Advisor در طی فرآیند بهینه سازی پارامترهای ورودی مختلف، فراخوانی میشود که در پاسخ به آنها عدد تخمینی (سود، سودآوری یا ویژگی دیگر) برمیگردد. این جمعیت در مورد Expert Advisor چیزی نمیداند (و نباید چیزی هم بداند). تنها وظیفه آن یافتن مقدار بهینه یک تابع هدف ناشناخته با مجموعه دلخواه آرگومان های عددی است. به همین دلیل ما از یک رابط انتزاعی یعنی کلاس Functor استفاده میکنیم.
class Functor { public: virtual double calculate(const double &vector[]) = 0; };
تنها متدی که آرایه ای از پارامترها را دریافت میکند و یک عدد را برمیگرداند (همه انواع double هستند). در آینده، EA باید به نوعی یک کلاس مشتق شده از Functor را پیاده سازی کند و متغیر مورد نیاز را در متد calculate محاسبه کند. بنابراین، اولین پارامتر متد”optimize ” یک شی با تابع بازگشتی ارائه شده توسط ربات معاملاتی را دریافت میکند.
پارامتر دوم متد ” optimize” حداکثر تعداد حلقه ها برای اجرای الگوریتم است. 3 پارامتر بعدی ضرایب PSO را تنظیم میکنند: ‘ inertia ‘ – حفظ سرعت ذره (سرعت معمولاً با مقادیر کمتر از 1 کاهش مییابد)، ‘selfBoost’ و ‘ ’groupBoost تعیین میکنند که ذره هنگام تنظیم جهت خود به بهترین موقعیتهای شناخته شده در تاریخچه ذره / گروه چقدر پاسخگو است.
اکنون که تمام پارامترها را بررسی کردیم، میتوانیم به سراغ الگوریتم PSO برویم. حلقههای بهینهسازی تقریباً به صورت کاملاً ساده شبه کد را به طور کامل دوباره تولید میکنند.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4) { double result = -DBL_MAX; ArrayInitialize(solution, 0); for(int c = 0; c < cycles && !IsStopped(); c++) // predefined number of cycles { for(int i = 0; i < _size && !IsStopped(); i++) // loop through all particles { for(int p = 0; p < _params; p++) // update particle position and speed { double r1 = MathRand() * 1.0 / 32767; double rg = MathRand() * 1.0 / 32767; particles[i].velocity[p] = inertia * particles[i].velocity[p] + selfBoost * r1 * (particles[i].best[p] - particles[i].position[p]) + groupBoost * rg * (groups[particles[i].group].optimum[p] - particles[i].position[p]); particles[i].position[p] = particles[i].position[p] + particles[i].velocity[p]; // make sure to keep the particle inside the boundaries of parameter space if(particles[i].position[p] < lows[p]) particles[i].position[p] = lows[p]; else if(particles[i].position[p] > highs[p]) particles[i].position[p] = highs[p]; // respect step size if(steps[p] != 0) { particles[i].position[p] = ((int)MathRound((particles[i].position[p] - lows[p]) / steps[p])) * steps[p] + lows[p]; } } // get the function value for the particle i particles[i].positionValue = f.calculate(particles[i].position); // update the particle's best value and position (if improvement is found) if(particles[i].positionValue > particles[i].bestValue) { particles[i].bestValue = particles[i].positionValue; ArrayCopy(particles[i].best, particles[i].position); } // update the group's best value and position (if improvement is found) if(particles[i].positionValue > groups[particles[i].group].getResult()) { groups[particles[i].group].assign(particles[i].positionValue); ArrayCopy(groups[particles[i].group].optimum, particles[i].position); // update the global maximum value and solution (if improvement is found) if(particles[i].positionValue > result) { result = particles[i].positionValue; ArrayCopy(solution, particles[i].position); } } } } return result; }
این روش حداکثر مقدار به دست آمده از تابع هدف را برمیگرداند. روش دیگر مختص خواندن مختصات است (مجموعه پارامترها).
bool getSolution(double &result[]) { ArrayCopy(result, solution); return !IsStopped(); }
این تقریباً کل الگوریتم PSO است. من قبلاً اشاره کردم که چند ساده سازی وجود دارد. اول از همه، ویژگی خاص زیر را در نظر بگیرید.
جهان گسسته بدون تکرار در الگوریتم PSO
برای محاسبه مجدد پویای مجموعه پارامترها،functor بارها و بارها فراخوانی میشود، اما هیچ تضمینی وجود ندارد که الگوریتم PSO چندین بار به همان نقطه برخورد نخواهد کرد، خصوصاً با توجه به دقت در محورها. برای جلوگیری از چنین برخوردی، لازم است به نحوی امتیازات محاسبه شده را شناسایی کرده و از آنها صرف نظر کنید.
پارامترها فقط اعداد یا دنباله ای از بایت ها هستند. مشهور ترین تکنیک برای بررسی منحصر به فرد بودن دادهها استفاده از هش است. محبوبترین راه برای به دست آوردن هش، CRC است. CRC یک عدد چک است (معمولاً یک عدد صحیح چند بیتی است) که بر اساس دادهها تولید میشود به گونهای که مطابقت دو عدد مشخص از مجموعه داده ها به معنی این است که به احتمال زیاد مجموعه ها یکسان است. هر چقدر بیت در CRC بیشتر باشد، احتمال همسان سازی بیشتر است (تقریباً تا 100٪). CRCی 64 بیتی احتمالاً برای کار ما کافی است. در صورت نیاز، میتوان آن را توسعه داد یا به تابع هش دیگری تغییر داد. پیاده سازی محاسبه CRC را میتوان به راحتی از C به MQL منتقل کرد. یکی از گزینه های ممکن در فایل crc64.mqh پیوست شده در زیر موجود است. تابع اصلی دارای نمونه اولیه است.
ulong crc64(ulong crc, const uchar &s[], int l);
CRC را از بلوک داده قبلی (اگر بیش از یک باشد یا اگر یک بلوک وجود داشته باشد 0 را مشخص میکند)، آرایهای از بایت ها و اطلاعات مربوط به تعداد عناصر پردازش شده در آن می پذیرد. این تابع CRC ی 64 بیتی را برمیگرداند.
ما باید مجموعه ای از پارامترها را وارد این تابع کنیم. اما این کار مستقیماً قابل انجام نیست، زیرا هر یک double است. برای تبدیل آن به یک آرایه بایت، اجازه دهید از کتابخانه TypeToBytes.mqh استفاده کنیم (فایل به مقاله پیوست شده است ؛ اما بهتر است کد پایه برای نسخه به روز آن را بررسی کنید).
بعد از گنجاندن این کتابخانه، می توان یک تابع wrapper برای محاسبه CRC64 از مجموعه ای از پارامترها ایجاد کرد:
#include <TypeToBytes.mqh> #include <crc64.mqh> template<typename T> ulong crc64(const T &array[]) { ulong crc = 0; int len = ArraySize(array); for(int i = 0; i < len; i++) { crc = crc64(crc, _R(array[i]).Bytes, sizeof(T)); } return crc; }
اکنون سوالات زیر به وجود می آیند: کجا باید هش ها را ذخیره کرد و چگونه میتوان خاص بودن آنها را بررسی کرد. مناسب ترین راه حل یک درخت باینری است. این یک ساختار داده است که عملکردهای سریعی را برای افزودن مقادیر جدید و بررسی وجود موارد اضافه شده فراهم میکند. سرعت زیاد توسط ویژگی خاص درختی به نام درخت متوازن تامین میشود. به عبارت دیگر، درخت باید متوازن باشد (باید دائماً در حالت تعادل نگه داشته شود) تا از حداکثر سرعت عملیات اطمینان حاصل شود. واقعیت خوب این است که ما از درخت برای ذخیره هش استفاده میکنیم. در اینجا تعریف هش آمده است.
تابع هش (الگوریتم تولید هش) برای هر داده ورودی مقدار خروجی توزیع شده یکنواخت ایجاد میکند. در نتیجه، افزودن یک هش به یک درخت باینری از نظر آماری وضعیت آن را نزدیک به متوازن فراهم میکند، و در نتیجه منجر به کارایی بالا میشود.
درخت باینری مجموعه ای از نودها است که هر کدام از آن ها حاوی مقدار مشخص و دو ارجاع اختیاری به اصطلاح نود راست و چپ هستند. مقدار نود سمت چپ همیشه کمتر از مقدار نود والد است؛ مقدار در نود سمت راست همیشه بیشتر از مقدار والد است. درخت با مقایسه یک مقدار جدید با مقادیر نود، از ریشه شروع به پر شدن میکند. اگر مقدار جدید برابر با مقدار ریشه (یا نود دیگر) باشد، علامت وجود مقدار در درخت برگردانده میشود. اگر مقدار جدید کمتر از مقدار نود است، به نود سمت چپ بروید و زیر درخت آن را به روشی مشابه پردازش کنید. اگر مقدار جدید بیشتر از مقدار نود است، زیر درخت راست را دنبال کنید. اگر هر یک از مراجع null باشد (به این معنی است که هیچ شاخه دیگری وجود ندارد)، جستجو بدون نتیجه انجام میشود. به همین دلیل، یک نود جدید با مقدار جدید باید به جای مرجع null ایجاد شود.
یک جفت کلاس الگو برای پیاده سازی این منطق ایجاد شده است: TreeNode و BinaryTree. کدهای کامل آنها در فایل هدر پیوست ارائه شده است.
template<typename T> class TreeNode { private: TreeNode *left; TreeNode *right; T value; public: TreeNode(T t): value(t) {} // adds new value into subtrees and returns false or // returns true if t exists as value of this node or in subtrees bool add(T t); ~TreeNode(); TreeNode *getLeft(void) const; TreeNode *getRight(void) const; T getValue(void) const; }; template<typename T> class BinaryTree { private: TreeNode<T> *root; public: bool add(T t); ~BinaryTree(); };
اگر مقدار از قبل در درخت وجود داشته باشد، متد ‘add’، true را برمیگرداند. اگر قبلاً وجود نداشته باشد اما به تازگی اضافه شده باشد، false را برمیگرداند. حذف یک ریشه در مخرب درخت به طور خودکار منجر به حذف تمام نودهای فرزند میشود.
کلاس درخت پیاده سازی شده یکی از ساده ترین انواع است. درختان پیشرفته دیگری نیز وجود دارند، بنابراین در صورت تمایل میتوانید آنها را جاسازی کنید.
اجازه دهید BinaryTree را به کلاس Swarm اضافه کنیم.
class Swarm { private: BinaryTree<ulong> index;
قسمت هایی از متد ” optimize ” که در آن ذرات را به موقعیت های جدید منتقل میکنیم باید گسترش یابد.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4) { // ... double next[]; ArrayResize(next, _params); for(int c = 0; c < cycles && !IsStopped(); c++) { int skipped = 0; for(int i = 0; i < _size && !IsStopped(); i++) { // new placement of particles using temporary array next for(int p = 0; p < _params; p++) { double r1 = MathRand() * 1.0 / 32767; double rg = MathRand() * 1.0 / 32767; particles[i].velocity[p] = inertia * particles[i].velocity[p] + selfBoost * r1 * (particles[i].best[p] - particles[i].position[p]) + groupBoost * rg * (groups[particles[i].group].optimum[p] - particles[i].position[p]); next[p] = particles[i].position[p] + particles[i].velocity[p]; if(next[p] < lows[p]) next[p] = lows[p]; else if(next[p] > highs[p]) next[p] = highs[p]; if(steps[p] != 0) { next[p] = ((int)MathRound(next[p] / steps[p])) * steps[p]; } } // check if the tree contains this parameter set and add it if not if(index.Add(crc64(next))) { skipped++; continue; } // apply new position to the particle ArrayCopy(particles[i].position, next); particles[i].positionValue = f.calculate(particles[i].position); // ... } Print("Cycle ", c, " done, skipped ", skipped, " of ", _size, " / ", result); if(skipped == _size) break; // full coverage }
ما آرایه کمکی ” next “را اضافه کردیم، جایی که ابتدا مختصات تازه ایجاد شده اضافه میشوند. CRC برای آنها محاسبه شده و منحصر به فرد بودن مقدار بررسی میشود. اگر موقعیت جدید هنوز پیدا نشده باشد، آن را به درخت اضافه میکنیم، در ذره مربوطه کپی میکنیم و تمام محاسبات لازم برای این موقعیت انجام میشود. اگر موقعیت از قبل در درخت وجود داشته باشد (یعنی، functor برای آن قبلاً محاسبه شده است)، از این تکرار صرف نظر میشود.
تست عملکرد اولیه در الگوریتم PSO
هر آن چه در بالا مورد بحث قرار گرفت حداقل مبنای لازم برای اجرای اولین آزمون ها است. برای اطمینان از این که بهینه سازی واقعاً کار میکند، اجازه دهید از اسکریپت testpso.mq5 استفاده کنیم. فایل هدر ParticleSwarmParallel.mqh فایل هدر مورد استفاده در این اسکریپت است که نه تنها شامل کلاس هایی است که از قبل آشنا بودند، بلکه شامل پیشرفتهای دیگری است که در زیر بررسی خواهیم کرد.
تست ها به سبک OOP طراحی شدهاند که به شما اجازه میدهد توابع هدف مورد علاقه خود را تنظیم کنید. کلاس پایه برای آزمون ها BaseFunctor است.
class BaseFunctor: public Functor { protected: const int params; double max[], min[], steps[]; public: BaseFunctor(const int p): params(p) // number of parameters { ArrayResize(max, params); ArrayResize(min, params); ArrayResize(steps, params); ArrayInitialize(steps, 0); PSOTests::register(&this); } virtual void test(const int loop) // worker method { Swarm swarm(params, max, min, steps); swarm.optimize(this, loop); double result[]; swarm.getSolution(result); for(int i = 0; i < params; i++) { Print(i, " ", result[i]); } } };
همه اشیای کلاس های مشتق شده با استفاده از روش ‘register’ در کلاس PSOTests به طور خودکار در زمان ایجاد ثبت می شوند.
class PSOTests { static BaseFunctor *testCases[]; public: static void register(BaseFunctor *f) { int n = ArraySize(testCases); ArrayResize(testCases, n + 1); testCases[n] = f; } static void run(const int loop = 100) { for(int i = 0; i < ArraySize(testCases); i++) { testCases[i].test(loop); } } };
تست ها (بهینه سازی) با استفاده از متد ” run ” اجرا میشود، که “test” را بر روی تمام اشیای ثبت شده فراخوانی میکند.
بسیاری از توابع محک محبوب، از جمله “” rosenbrock ، “griewank” ، ” sphere ” وجود دارد که در اسکریپت اجرا میشوند. به عنوان مثال، دامنه جستجو و متد ” calculate ” برای یک sphere میتواند به شرح زیر تعریف شود.
class Sphere: public BaseFunctor { public: Sphere(): BaseFunctor(3) // expected global minimum (0, 0, 0) { for(int i = 0; i < params; i++) { max[i] = 100; min[i] = -100; } } virtual void test(const int loop) { Print("Optimizing " + typename(this)); BaseFunctor::test(loop); } virtual double calculate(const double &vec[]) { int dim = ArraySize(vec); double sum = 0; for(int i = 0; i < dim; i++) sum += pow(vec[i], 2); return -sum; // negative for maximization } };
توجه داشته باشید که توابع استاندارد محک از مینیمم سازی استفاده میکنند، در حالی که ما یک الگوریتم PSO مبتنی بر ماکزیمم سازی را پیاده سازی کردیم (زیرا هدف ما جستجوی ماکزیمم عملکرد EA است). به همین دلیل، از نتیجه محاسبه با علامت منفی استفاده خواهد شد. همچنین، ما در این جا از مرحله گسسته استفاده نمیکنیم، بنابراین توابع پیوسته هستند.
void OnStart()
{
PSOTests::Sphere sphere;
PSOTests::Griewank griewank;
PSOTests::Rosenbrock rosenbrock;
PSOTests::run();
}
با اجرای اسکریپت، میبینید که مقادیر مختصات نزدیک به راهحل دقیق (extremeum) را ثبت میکند. از آن جا که ذرات به صورت تصادفی مقداردهی میشوند، هر اجرا، مقادیر کمی متفاوت تولید میکند. دقت راهحل به پارامترهای ورودی الگوریتم بستگی دارد.
Optimizing PSOTests::Sphere PSO[3] created: 15/3 PSO Processing... Cycle 0 done, skipped 0 of 15 / -1279.167775306995 Cycle 10 done, skipped 0 of 15 / -231.4807406906516 Cycle 20 done, skipped 0 of 15 / -4.269510657558273 Cycle 30 done, skipped 0 of 15 / -1.931949742316357 Cycle 40 done, skipped 0 of 15 / -0.06018744740061506 Cycle 50 done, skipped 0 of 15 / -0.009498109984732127 Cycle 60 done, skipped 0 of 15 / -0.002058433538555499 Cycle 70 done, skipped 0 of 15 / -0.0001494176502579518 Cycle 80 done, skipped 0 of 15 / -4.141817579039349e-05 Cycle 90 done, skipped 0 of 15 / -1.90930142126799e-05 Cycle 99 done, skipped 0 of 15 / -8.161728746514931e-07 PSO Finished 1500 of 1500 planned calculations: true 0 -0.000594423827318461 1 -0.000484001094843528 2 0.000478096358862763 Optimizing PSOTests::Griewank PSO[2] created: 10/3 PSO Processing... Cycle 0 done, skipped 0 of 10 / -26.96927938978973 Cycle 10 done, skipped 0 of 10 / -0.939220906325796 Cycle 20 done, skipped 0 of 10 / -0.3074442362962919 Cycle 30 done, skipped 0 of 10 / -0.121905607345751 Cycle 40 done, skipped 0 of 10 / -0.03294107382891465 Cycle 50 done, skipped 0 of 10 / -0.02138355984774098 Cycle 60 done, skipped 0 of 10 / -0.01060479828529859 Cycle 70 done, skipped 0 of 10 / -0.009728742850384609 Cycle 80 done, skipped 0 of 10 / -0.008640623678293768 Cycle 90 done, skipped 0 of 10 / -0.008578769833161193 Cycle 99 done, skipped 0 of 10 / -0.008578769833161193 PSO Finished 996 of 1000 planned calculations: true 0 3.188612982502877 1 -4.435728146291838 Optimizing PSOTests::Rosenbrock PSO[2] created: 10/3 PSO Processing... Cycle 0 done, skipped 0 of 10 / -19.05855349617553 Cycle 10 done, skipped 1 of 10 / -0.4255148824156119 Cycle 20 done, skipped 0 of 10 / -0.1935391314277153 Cycle 30 done, skipped 0 of 10 / -0.006468452482022688 Cycle 40 done, skipped 0 of 10 / -0.001031992354315317 Cycle 50 done, skipped 0 of 10 / -0.00101322411502283 Cycle 60 done, skipped 0 of 10 / -0.0008800704421316765 Cycle 70 done, skipped 0 of 10 / -0.0005593151578155307 Cycle 80 done, skipped 0 of 10 / -0.0005516786893301249 Cycle 90 done, skipped 0 of 10 / -0.0005473814163781119 Cycle 99 done, skipped 0 of 10 / -7.255520122486163e-06 PSO Finished 982 of 1000 planned calculations: true 0 1.001858172119364 1 1.003524791491219
توجه داشته باشید که اندازه ازدحام و تعداد گروهها (در log نوشته شده است در خطوطی مانند PSO[N] ایجاد شده: X / G، جایی كه N بعد فضایی است، X تعداد ذرات است، G تعداد گروهها است) به طور خودکار مطابق با قوانین برنامهریزی شده بر اساس دادههای ورودی انتخاب میشود.
حرکت به دنیای موازی در الگوریتم PSO
اولین آزمون خوب است. با این حال، این یک تفاوت ظریف دارد – چرخه شمارش ذرات در یک نخ واحد انجام می شود، در حالی که ترمینال امکان استفاده از تمام هستههای پردازنده را فراهم میکند. هدف نهایی ما نوشتن یک موتور بهینه سازی PSO است که میتواند در EA برای بهینه سازی چند رشته ای در تستر MetaTrader تعبیه شود و بنابراین یک جایگزین برای الگوریتم ژنتیک استاندارد ارائه دهد.
با انتقال مکانیکی الگوریتم درون EA به جای اسکریپت، نمیتوان محاسبات را موازی کرد. این مستلزم اصلاح الگوریتم PSO است.
اگر به کد موجود نگاه کنید، این وظیفه، انتخاب گروه هایی از ذرات را برای محاسبات موازی پیشنهاد میکند. هر گروه میتواند به طور مستقل پردازش شود. یک چرخه کامل برای تعداد دفعات مشخص شده در داخل هر گروه انجام میشود.
برای جلوگیری از اصلاح هسته کلاس “” Swarm، بیایید از یک راه حل ساده استفاده کنیم: به جای چندین گروه در داخل کلاس، چندین نمونه کلاس ایجاد خواهیم کرد که در هر کدام، تعداد گروهها از بین میرود، یعنی برابر با یک. علاوه بر این، ما باید کدی را ارائه دهیم که به نمونه ها امکان تبادل اطلاعات را بدهد، زیرا هر نمونه روی عامل آزمایش خود اجرا میشود.
ابتدا اجازه دهید روش جدیدی را برای مقداردهی اولیه اضافه کنیم.
Swarm(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { if(MQLInfoInteger(MQL_OPTIMIZATION)) { init(size == 0 ? params * AUTO_SIZE_FACTOR : size, 1, params, max, min, step); } ...
با توجه به عملکرد برنامه در حالت بهینه سازی، تعداد گروه ها را برابر با 1 تنظیم کنید. اندازه ازدحام پیش فرض با یک قانون کلی تعیین میشود (مگر اینکه پارامتر “size” صریحاً روی مقداری غیر از 0 تنظیم شود).
در کنترل کننده رویداد OnTester ، Expert Advisor میتواند نتیجه یک mini-swarm (متشکل از تنها یک نود) را با استفاده از تابع getSolution به دست آورد و آن را در یک فریم به ترمینال ارسال کند. ترمینال میتواند passها را آنالیز کرده و بهترین را انتخاب کند. از نظر منطقی، تعداد ازدحام / گروه های موازی باید برابر حداقل تعداد هسته ها باشد. با این حال، میتواند بالاتر باشد (اگرچه باید سعی کنید چندین برابر آن باشد). هرچه ابعاد فضا بزرگتر باشد، ممکن است به گروههای بیشتری نیز نیاز باشد. اما تعداد هسته ها باید برای آزمایشهای ساده کافی باشد.
برای محاسبه فضای بدون امتیاز تکراری، تبادل داده بین نمونهها مورد نیاز است. همانطور که به یاد دارید، لیست نقاط پردازش شده در هر شی در درخت باینری ” ” index ذخیره میشود. همانند نتایج، میتواند در یک فریم به ترمینال ارسال شود، اما مشکل این است که رجیستری ترکیب فرضی این لیست ها نمیتواند به عامل های آزمایش برگردانده شود. متأسفانه، معماری تستر از انتقال کنترل شده اطلاعات فقط از طریق عاملها به ترمینال پشتیبانی میکند اما نه به عقب. وظایف حاصل از ترمینال در قالب بسته به عوامل توزیع میشود.
بنابراین، من تصمیم گرفتم فقط از عامل های محلی استفاده کنم و شاخصهای هر گروه را در فایلهای یک فولدر مشترک (FILE_COMMON) ذخیره کنم. هر عامل، شاخص خود را مینویسد و میتواند شاخصهای سایر پاس ها را در هر زمان بخواند، و همچنین آنها را به شاخص خود اضافه کند. این میتواند در هنگام راه اندازی اولیه مورد نیاز باشد.
درMQL ، فقط در صورت بسته بودن فایل، تغییرات در فایل نوشته شده توسط سایر فرایندها قابل خواندن است. فلگ های FILE_SHARE_READ، FILE_SHARE_WRITE و توابع FileFlush در اینجا کمکی نمیکنند.
پشتیبانی از نوشتن شاخصها با استفاده از الگوی معروف “visitor” اجرا میشود.
template<typename T> class Visitor { public: virtual void visit(TreeNode<T> *node) = 0; };
رابط مینیمالیستی آن اعلام میکند که ما قصد داریم عملکرد دلخواهی با نود درخت عبور داده شده انجام دهیم. یک پیاده سازی خاص جایگزین برای کار با فایل ها ایجاد شده است: Exporter. مقدار داخلی هر نود به ترتیب پیمایش کل درخت توسط مرجع، در یک خط جداگانه در فایل ذخیره می شود.
template<typename T> class Exporter: public Visitor<T> { private: int file; uint level; public: Exporter(const string name): level(0) { file = FileOpen(name, FILE_READ | FILE_WRITE | FILE_CSV | FILE_ANSI | FILE_SHARE_READ| FILE_SHARE_WRITE | FILE_COMMON, ','); } ~Exporter() { FileClose(file); } virtual void visit(TreeNode<T> *node) override { #ifdef PSO_DEBUG_BINTREE if(node.getLeft()) visit(node.getLeft()); FileWrite(file, node.getValue()); if(node.getRight()) visit(node.getRight()); #else const T v = node.getValue(); FileWrite(file, v); level++; if((level | (uint)v) % 2 == 0) { if(node.getLeft()) visit(node.getLeft()); if(node.getRight()) visit(node.getRight()); } else { if(node.getRight()) visit(node.getRight()); if(node.getLeft()) visit(node.getLeft()); } level--; #endif } };
پیمایش درخت مرتب شده، که منطقی تر به نظر میرسد، فقط در صورت debugging میتواند مورد استفاده قرار گیرد، در صورتی که برای مقایسه متنی نیاز به دریافت سطر های مرتب شده در داخل فایلها دارید. این روش توسط دستورالعمل تدوین مشروط PSO_DEBUG_BINTREE احاطه شده است و به طور پیش فرض غیرفعال است. در عمل، توازن آماری درخت با افزودن مقادیر تصادفی و توزیع شده یکنواخت ذخیره شده در درخت (هش ها) تضمین میشود. اگر عناصر درخت به شکل مرتب سازی شده ذخیره شوند، در هنگام بارگذاری آن از فایل، به کمترین و بهینه ترین تنظیمات (یک شاخه بلند یا یک لیست) خواهیم رسید. برای جلوگیری از این امر، در مرحله ذخیره درخت، عدم اطمینان در مورد توالی پردازش نود ها ایجاد میشود.
روش ویژه ذخیره درخت به visitor عبور داده شده را میتوان با استفاده از کلاس Explorer به راحتی به کلاس BinaryTree اضافه کرد.
template<typename T> class BinaryTree { ... void visit(Visitor<T> *visitor) { visitor.visit(root); } };
برای اجرای عملیات، روش جدیدی در کلاس Swarm نیز لازم است.
void exportIndex(const int id) { const string name = sharedName(id); Exporter<ulong> exporter(name); index.visit(&exporter); }
پارامتر ‘id’ به معنی یک عدد pass منحصر به فرد (برابر با شماره گروه) است. از این پارامتر برای پیکربندی بهینه سازی در تستر استفاده خواهد شد. روش exportIndex را باید بلافاصله پس از اجرای دو روش ازدحام فراخوانی کنید: بهینه سازی و getSolution. این کار توسط یک کد فراخوانی انجام میشود ، زیرا ممکن است همیشه لازم نباشد: اولین مثال “موازی” ما (به ادامه مطلب مراجعه کنید) نیازی به آن ندارد. اگر تعداد گروهها با تعداد هسته ها برابر باشد، آنها قادر به تبادل اطلاعات نخواهند بود، زیرا به طور موازی راه اندازی میشوند و خواندن فایل درون حلقه کارآمد نیست.
تابع کمکی sharedName، که در داخل exportIndex ذکر شده است، ایجاد یک نام منحصر به فرد را بر اساس شماره گروه، نام EA و پوشه ترمینال امکان پذیر میکند.
#define PPSO_FILE_PREFIX "PPSO-" string sharedName(const int id, const string prefix = PPSO_FILE_PREFIX, const string ext = ".csv") { ushort array[]; StringToShortArray(TerminalInfoString(TERMINAL_PATH), array); const string program = MQLInfoString(MQL_PROGRAM_NAME) + "-"; if(id != -1) { return prefix + program + StringFormat("%08I64X-%04d", crc64(array), id) + ext; } return prefix + program + StringFormat("%08I64X-*", crc64(array)) + ext; }
اگر یک شناسه برابر با -1 به تابع منتقل شود، تابع یک mask ایجاد میکند تا تمام فایلهای این نمونه ترمینال را پیدا کند. این ویژگی هنگام حذف فایلهای موقت قدیمی (از بهینه سازی قبلی این Expert Advisorrt) و همچنین هنگام خواندن فهرستهای جریانهای موازی استفاده میشود. در اینجا نحوه انجام آن به صورت کلی آمده است.
هر فایل پیدا شده برای پردازش به کلاس جدید FileReader منتقل میشود. کلاس، وظیفه باز کردن فایل در حالت خواندن را بر عهده دارد. همچنین به طور متوالی تمام خطوط را بارگیری کرده و بلافاصله آنها را به رابط Feed منتقل میکند.
همانطور که حدس میزنید ، رابط Feed باید مستقیماً در ازدحام اجرا شود، زیرا ما این را از داخل FileReader عبور دادیم.
class Swarm: public Feed { private: ... int _read; int _unique; int _restored; BinaryTree<ulong> merge; public: ... virtual bool feed(const int dump) override { const ulong value = (ulong)FileReadString(dump); _read++; if(!index.add(value)) _restored++; // just added into the tree else if(!merge.add(value)) _unique++; // was already indexed, hitting _unique in total return true; } ...
با استفاده از متغیرهای _read ، _unique و _restored ، روش تعداد کل عناصر خوانده شده (از تمام فایلها)، تعداد عناصر اضافه شده به فهرست و تعداد عناصر اضافه نشده (که قبلاً در فهرست هستند) محاسبه میکند. از آنجا که گروهها به طور مستقل کار میکنند، شاخصهای گروههای مختلف میتوانند تکراری باشند.
این آمار در تعیین لحظه ای که فضای جستجو به طور کامل کاوش شده یا نزدیک به کاوش کامل است مهم است. در این حالت ، تعداد _unique به تعداد ترکیبات ممکن پارامتر نزدیک میشود.
با افزایش تعداد passهای تکمیل شده، امتیازات بی نظیر بیشتری از تاریخ مشترک در فهرستهای محلی بارگیری میشوند. پس از اجرای بعدی “محاسبه” ، ایندکس نقاط جدیدی را بررسی میکند و اندازه فایلهای ذخیره شده دائماً رشد میکند. به تدریج ، همپوشانی عناصر در فایلها شروع به غلبه میکند. این امر به برخی هزینههای اضافی نیاز دارد که با این وجود کمتر از محاسبه مجدد فعالیت تجاری EA است. با نزدیک شدن پردازش به پوشش کامل فضای بهینه سازی ، این امر منجر به تسریع چرخه های PSO با پردازش هر یک از گروههای بعدی (وظایف تستر) خواهد شد.
نمودار کلاس بهینه سازی ازدحام ذرات
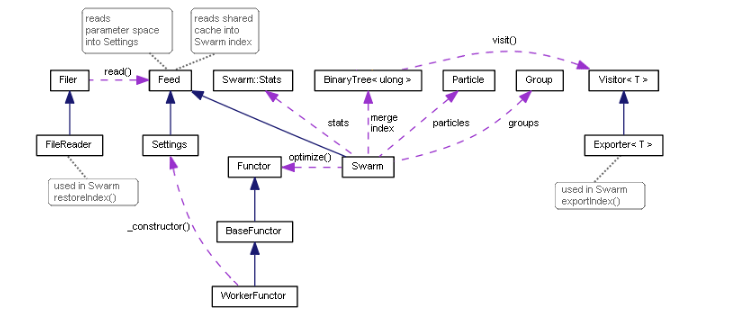
تست محاسبات موازی در الگوریتم PSO
برای آزمایش عملکرد الگوریتم در چندین نخ، اجازه دهید اسکریپت قدیمی را به PspO.mq5 Expert Advisor تبدیل کنیم. این در حالت محاسبه ریاضی اجرا خواهد شد، زیرا هنوز فضای معامله لازم نیست.
مجموعه توابع آزمون هدف یکسان است، همچنین کلاسهایی که آنها را اجرا میکنند عملاً بدون تغییر هستند. یک آزمون خاص در متغیرهای ورودی انتخاب خواهد شد.
enum TEST { Sphere, Griewank, Rosenbrock }; sinput int Cycles = 100; sinput TEST TestCase = Sphere; sinput int SwarmSize = 0; input int GroupCount = 0;
در اینجا میتوانیم تعداد چرخهها، اندازه ازدحام و تعداد گروهها را نیز مشخص کنیم. همه اینها در پیادهسازی functor ، به ویژه در سازنده Swarm استفاده میشود. مقادیر صفر پیش فرض به معنای انتخاب خودکار بر اساس بُعد کار است.
class BaseFunctor: public Functor { protected: const int params; double max[], min[], steps[]; double optimum; double result[]; public: ... virtual void test() { Swarm swarm(SwarmSize, GroupCount, params, max, min, steps); optimum = swarm.optimize(this, Cycles); swarm.getSolution(result); } double getSolution(double &output[]) const { ArrayCopy(output, result); return optimum; } };
تمام محاسبات از OnTester handler شروع میشود. از پارامتر GroupCount (که به وسیله آن تکرار تسترها سازماندهی میشوند) به عنوان یک تصادفی ساز استفاده میشود تا اطمینان حاصل شود که نخها در رشتههای مختلف حاوی ذرات مختلف هستند. بسته به پارامتر TestCase یک test functor ایجاد میشود. بعد، روش ()functor.test فراخوانی میشود، پس از آن میتوان نتایج را با استفاده از () functor.getSolution خوانده و میتوان آن را در یک فریم به ترمینال ارسال کرد.
double OnTester() { MathSrand(GroupCount); // reproducible randomization BaseFunctor *functor = NULL; switch(TestCase) { case Sphere: functor = new PSOTests::Sphere(); break; case Griewank: functor = new PSOTests::Griewank(); break; case Rosenbrock: functor = new PSOTests::Rosenbrock(); break; } functor.test(); double output[]; double result = functor.getSolution(output); if(MQLInfoInteger(MQL_OPTIMIZATION)) { FrameAdd("PSO", 0xC0DE, result, output); } else { Print("Solution: ", result); for(int i = 0; i < ArraySize(output); i++) { Print(i, " ", output[i]); } } delete functor; return result; }
یک دسته از توابع OnTesterInit ، OnTesterPass ، OnTesterDeinit در ترمینال کار میکنند. این فریمها را جمع آوری میکند و بهترین راهحل را از راهحلهای ارسال شده تعیین میکند.
int passcount = 0; double best = -DBL_MAX; double location[]; void OnTesterPass() { ulong pass; string name; long id; double r; double data[]; while(FrameNext(pass, name, id, r, data)) { // compare r with all other passes results if(r > best) { best = r; ArrayCopy(location, data); } Print(passcount, " ", id); const int n = ArraySize(data); ArrayResize(data, n + 1); data[n] = r; ArrayPrint(data, 12); passcount++; } } void OnTesterDeinit() { Print("Solution: ", best); ArrayPrint(location); }
دادههای زیر برای ورود به سیستم نوشته شده است: شمارنده عبور، شماره توالی آن (هنگامی که یک رشته به دلیل تفاوت در دادهها از یک نخ دیگر عبور میکند، ممکن است در کارهای پیچیده متفاوت باشد)، مقدار تابع هدف و پارامترهای مربوطه تصمیم نهایی در OnTesterDeinit گرفته شده است.
همچنین اجازه دهید Expert Advisory نه تنها در تستر بلکه در یک نمودار منظم نیز فعال شود. در این حالت، الگوریتم PSO در حالت تک نخی منظم اجرا میشود.
int OnInit() { if(!MQLInfoInteger(MQL_TESTER)) { EventSetTimer(1); } return INIT_SUCCEEDED; } void OnTimer() { EventKillTimer(); OnTester(); }
بگذارید ببینیم چگونه کار میکند مقادیر زیر از پارامترهای ورودی استفاده خواهد شد:
- Cycles — 100 ؛
- TestCase – Griewank ؛
- SwarmSize – 100 ؛
- GroupCount — 10 ؛
هنگام راه اندازی یک Expert Advisor در نمودار، گزارش زیر نوشته خواهد شد.
Successive PSO of Griewank PSO[2] created: 100/10 PSO Processing... Cycle 0 done, skipped 0 of 100 / -1.000317162069485 Cycle 10 done, skipped 0 of 100 / -0.2784790501384311 Cycle 20 done, skipped 0 of 100 / -0.1879188508394087 Cycle 30 done, skipped 0 of 100 / -0.06938172138150922 Cycle 40 done, skipped 0 of 100 / -0.04958694402304631 Cycle 50 done, skipped 0 of 100 / -0.0045818974357138 Cycle 60 done, skipped 0 of 100 / -0.0045818974357138 Cycle 70 done, skipped 0 of 100 / -0.002161613760466419 Cycle 80 done, skipped 0 of 100 / -0.0008991629607246754 Cycle 90 done, skipped 0 of 100 / -1.620636881582982e-05 Cycle 99 done, skipped 0 of 100 / -1.342285474092986e-05 PSO Finished 9948 of 10000 planned calculations: true Solution: -1.342285474092986e-05 0 0.004966759354110293 1 0.002079707592422949
از آنجا که موارد آزمایشی به سرعت محاسبه میشوند (ظرف یک یا دو ثانیه)، اندازه گیری زمان، منطقی نیست. بعداً برای کارهای واقعی معامله اضافه خواهد شد.
اکنون، EA را در تستر انتخاب کنید، “محاسبات ریاضی” را در لیست “”Modeling تنظیم کنید، از پارامترهای فوق به جز GroupCount برای EA استفاده کنید. این پارامتر برای بهینه سازی استفاده خواهد شد. بنابراین، مقادیر اولیه و نهایی را برای آن تنظیم کنید، بگذارید بگوییم 0 و 3 ، با یک مرحله 1 ، برای تولید 4 گروه لازم است (برابر با تعداد هسته). اندازه همه گروهها 100 خواهد بود (SwarmSize ، کل گروه). با وجود تعداد هستههای پردازنده کافی است (اگر همه گروهها به طور موازی بر روی عوامل کار کنند)، این نباید بر کارایی تأثیر بگذارد، بلکه از طریق بررسیهای اضافی فضای بهینه سازی، دقت راهحل را افزایش میدهد. گزارش زیر را میتوان دریافت کرد:
Parallel PSO of Griewank -12.550070232909 -0.002332638407 -0.039510275469 -3.139749741924 4.438437934965 -0.007396077598 3.139620588383 4.438298282495 -0.007396126543 0.000374731767 -0.000072178955 -0.000000071551 Solution: -7.1550806279852e-08 (after 4 passes) 0.00037 -0.00007
بنابراین، اطمینان حاصل کردیم که اصلاح موازی الگوریتم PSO در تستر در حالت بهینه سازی در دسترس قرار گرفته است. اما تاکنون فقط یک آزمون با استفاده از محاسبات ریاضی بوده است. در مرحله بعد، اجازه دهید PSO را برای بهینه سازی Expert Advisors در یک فضای معاملهای وفق دهیم.
برای مطالعه ادامه این مقاله روی لینک زیر کلیک کنید:
این مقاله ترجمه شده توسط تیم آکادمی ایران ام کیو ال می باشد.





پاسخها