در این مقاله قصد داریم شما را با مفهوم الگوهای بازاری به کمک ام کیو ال آشنا کنیم. از رویکرد های بازار مالی میتوان به همبستگی خودکار ، نقشه های حرارتی و نمودار توزیع اشاره کرد . به عبارت دیگر ما با استفاده از این الگو ها می توانیم به میزان افزایش یا کاهش قیمت در بازار مالی دست پیدا کنیم.

آکادمی ایران ام کیو ال در این مقاله به مفاهیم اصلی حافظه بازار ، الگو های فصلی در بازار ، رابطه همبستگی کاهشی و افزایش در فصول مختلف ،رویکرد های اکومومتری کلاسیکی و … می پردازد. اگر شما هم به دنبال یادگیری این اصول هستید پیشنهاد میکنیم با تا انتهای این مقاله همراه باشید.

بیشتر بخوانید : 3 ویژگی منحصر به فرد MQL5 | آشنایی بیشتر با ویژگی­ های زبان MQL5

مهمترین پیش نیاز های لازم برای ایجاد یک مدل و نمودار جدید (در زبان ام کیو ال)

در ابتدای مقاله، مفهوم حافظه بازار را تعریف می نماییم که به معنی وابستگی بلند مدت افزایش قیمتی برخی از سفارشات می باشد. سپس به مفهوم الگوهای فصلی می پردازیم که در بازارها وجود دارند. تا کنون، این دو مفهوم به صورت جداگانه وجود داشته اند. هدف این مقاله نشان دادن حافظه بازار به عنوان بخشی از طبیعت فصلی می باشد که از طریق همبستگی مضاعف افزایش یک سفارش دلخواه در بازه های زمانی نزدیک به هم و از طریق همبستگی کاهشی فواصل زمانی بیان می شود.

به فرضیه زیر توجه کنیم:

همبستگی افزایش قیمت به وجود الگوهای فصلی، به اندازه افزایش های کوتاه مدت، وابسته است.

اکنون به تایید یا تکذیب آن از طریق روش شهودی و کمی هم محاسباتی می پردازیم.

رویکرد اکونومتری کلاسیک برای تعیین الگوهای افزایش قیمت همبسته هستند.

مطابق رویکرد کلاسیک، عدم حضور الگوهای افزایش قیمت به وسیله نبود همبستگی سریالی بیان می شود. اگر همبستگی وجود نداشته باشد، مجموعه ای از افزایشه ها به صورت تصادفی در نظر گرفته می شوند د ر حالی که از بی تاثیر بودن جستجوهای بعدی برای الگوها مطمین باشیم.

حال نمونه ای از آنالیز بصری افزایش EURUSD با استفاده از تابع همبستگی را ببینیم. تمامی مثال ها با استفاده از IPython اجرا خواهند شد.

def standard_autocorrelation(symbol, lag):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') 
    rates = rates.diff(lag).dropna()
    from pandas.plotting import autocorrelation_plot
    plt.figure(figsize=(10, 5))
    autocorrelation_plot(rates)
standard_autocorrelation('EURUSD', 50)

این تابع قیمت های نزدیک بهم H1 را در دوره های مشخص (فاصله 50 استفاده شده است) به اختلافات مرتبط تبدیل می کند و نمودار همبستگی را نمایش می دهد.

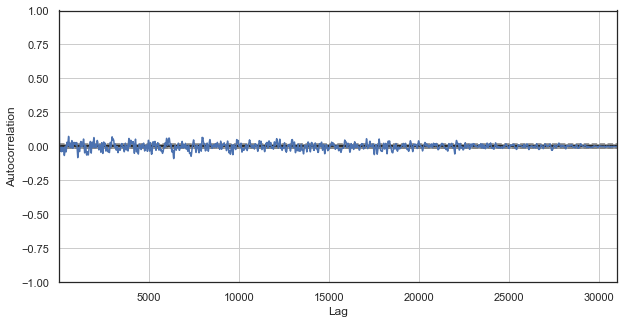
بررسی نمودار همبستگی خودکار ( ام کیو ال )

نمودار همبستگی خودکار هیچ الگویی در افزایش قیمت به دست نمی دهد. همبستگی های بین افزایش های متوالی در حدود صفر نوسان دارد که به تصادفی بودن سری های زمانی اشاره دارد. می توانیم تحلیل اکونومتری خود را در اینجا با نتیجه گیری تصادفی بودن بازار، به پایان برسانیم. با این وجود، پیشنهاد می کنم، تابع همبستگی از زاویه دیگری مجددا بررسی شود: در محدوده الگوهای فصلی.

حتما ثبت نام کنید : آموزش صفر تا صد Mql5

فرض می کنیم، همبستگی افزایش قیمت می تواند با وجود الگوهای فصلی تولید شود. بنابراین، از مثال تمامی ساعت ها به جز یک ساعت معین را خارج می کنیم. در نتیجه، یک سری زمانی جدید خواهیم ساخت که خصوصیات مختص به خود را دارد. یک تابع همبستگی برای این سری ها بسازید:

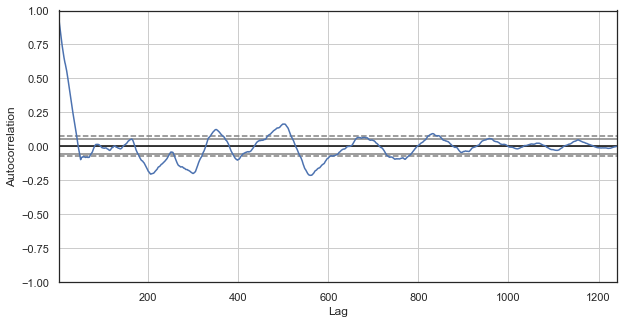
دیاگرام همبستگی برای سری های جدید بهتر به نظر می رسد. وابستگی شدیدی بین افزایش جدید با افزایش قبلی اش وجود دارد. وابستگی با افزایش دلتای زمانی کاهش می یابد. این امر یعنی اینکه افزایش در اولین ساعت کنونی به شدت با افزایش اولین ساعت روز قبل مرتبط است. این اطلاعات خیلی مهم وجود الگوهای فصلی را روشن می کند؛ یعنی افزایش ها حافظه دارند.

حتما ثبت نام کنید : آموزش بیشرفته mql4

الگوهای افزایش قیمت ( ام کیو ال )

رویکرد دلخواه برای تعیین الگوهای افزایش قیمت همبستگی خودکار فصلی است

دریافتیم که همبستگی بین افزایش اولین ساعت کنونی و روز قبل وجود دارد که با این وجود، با افزایش فاصله زمانی روزها کاهش می یابد. حال ببینیم که آیا همبستگی بین ساعت های متوالی وجود دارد یا خیر. بدین منظور، کد را بهینه می کنیم:

def seasonal_autocorrelation(symbol, lag, hour1, hour2):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') 
    rates = rates.drop(rates.index[~rates.index.hour.isin([hour1, hour2])]).diff(lag).dropna()
    from pandas.plotting import autocorrelation_plot
    plt.figure(figsize=(10, 5))
    autocorrelation_plot(rates)
seasonal_autocorrelation('EURUSD', 50, 1, 2)

در اینجا، تمامی ساعات را به غیر از اولین و دومین ساعت حذف می کنیم و سپس اختلاف سری های جدید را محاسبه نموده و تابع همبستگی خودکار را می سازیم:

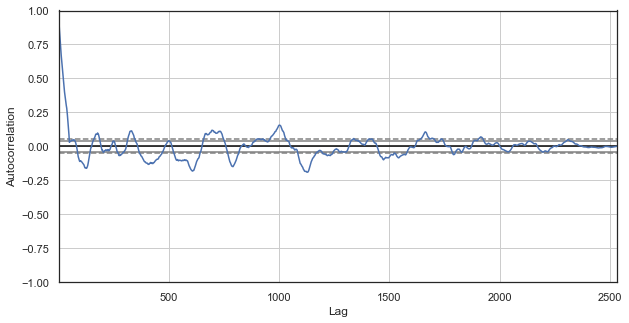
به وضوح، باز هم همبستگی زیادی بین نزدیک ترین ساعت ها وجود دارد که این امر همبستگی و تاثیر مرتبط بهم آنها را بیان می دارد. آیا می توانیم یک شاخص مرتبط قابل اعتماد برای تمام ساعت های جفتی ، نه ساعت های منتخب، به دست آوریم؟ برای این منظور، روش های مشروح زیر را به کار می بریم.

نقشه حرارتی همبستگی های فصلی برای تمامی ساعات

جستجوی بازار را ادامه میدهیم و به تایید فرضیه اصلی می پردازیم. نگاهی به تصویر کلی می اندازیم. تابع زیر مرتبا ساعت ها را از سری های زمانی حذف و فقط یک ساعت را باقی می گذارد. این تابع تفاوت قیمت را برای این سری ها ساخته و همبستگی آن را با سری های ساخته شده برای ساعات دیگر بیان میکند:

#calculate correlation heatmap between all hours
def correlation_heatmap(symbol, lag, corrthresh):
    out = pd.DataFrame()
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') 
    for i in range(24):
        ratesH = None
        ratesH = rates.drop(rates.index[~rates.index.hour.isin([i])]).diff(lag).dropna()
        out[str(i)] = ratesH['close'].reset_index(drop=True)
    plt.figure(figsize=(10, 10))
    corr = out.corr()
    # Generate a mask for the upper triangle
    mask = np.zeros_like(corr, dtype=np.bool)
    mask[np.triu_indices_from(mask)] = True
    sns.heatmap(corr[corr >= corrthresh], mask=mask)
    return out
out = correlation_heatmap(symbol='EURUSD', lag=25, corrthresh=0.9)

تابع سفارش افزایش (تاخیر زمانی) را، به اندازه آستانه همبستگی، به منظور حذف ساعت های دارای همبستگی پایین می پذیرد. نتیجه به شرح زیر می باشد:

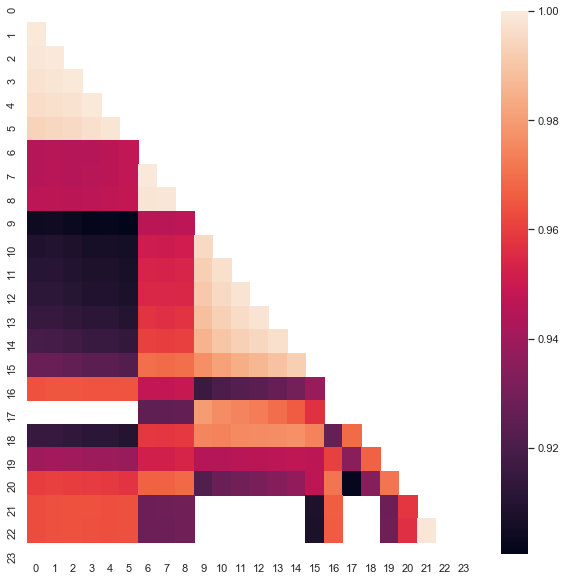
روشن است که این دسته بندی ها بیشترین همبستگی را دارند: ساعات 0 تا 5 و 10 تا 14. در مقاله قبلی یک سیستم تجاری بر اساس اولین دسته ساختیم که به روشی متفاوت (با استفاده از نمودار جعبه ای) پیدا شده بودند. اکنون الگوها نیز بر روی نقشه حرارتی قابل مشاهده هستند. حال دومین دسته جالب را ببینیم و آن را تحلیل کنیم. در اینجا خلاصه ای از آمارهای این دسته را ارائه می دهیم:

out[['10','11','12','13','14']].describe()

پارامتر های زمان برای تحلیل افزایش قیمت در بازار به کمک ام کیو ال

پارامترهای تمامی دسته های زمانی کاملا نزدیک بهم می باشند، اگرچه مقدار متوسط آنها برای مثال تحلیل شده منفی است (در حدود 100 در 5 رقم اعشار). یک تغییر در افزایش های متوسط بیان می دارد که بازار در طول این ساعات تمایل بیشتری به کاهش دارد تا اینکه افزایش یابد. همچنین شایان ذکر است که یک افزایش در تاخیر افزایش ها منجر به همبستگی بیشتر بین ساعتها به دلیل حضور یک جز انحرافی می گردد در حالیکه کاهش در تاخیر منجر به مقادیر کمتر می شود. با این وجود سازماندهی متناسب دسته ها تقریبا بدون تغییر می ماند.

به عنوان مثال، برای یک تاخیر مجزا، افزایش های 12، 13 و 14 همچنان همبستگی شدیدی دارند:

plt.figure(figsize=(10,5))
plt.plot(out[['12','13','14']])
plt.legend(out[['12','13','14']])
plt.show()

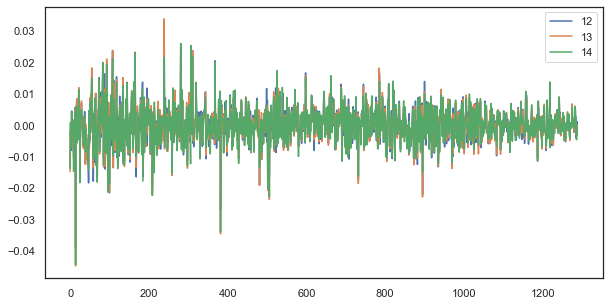
فرمول همیشگی: ساده اما خوب

همبستگی افزایش قیمت به وجود الگوهای فصلی، به اندازه افزایش های کوتاه مدت، وابسته است.

در دیاگرام همبستگی خودکار و نیز بر روی نقشه حرارتی دیدیم که وابستگی افزایش ساعتی بر روی مقادیر افزایش قبلی و نیز ساعت های متوالی وجود دارد. اولین نمود از تکرار اتفاقات در بعضی از ساعات روز ریشه می گیرد. دومین نمود با دسته بندی تغییر پذیری در برخی از دوره های زمانی مرتبط است. هر دوی این نتایج باید جداگانه در نظر گرفته شوند و در صورت امکان باید با هم ترکیب شوند. در این مقاله، مطالعه دیگری بر روی وابستگی در افزایش زمانی خاص (با حذف سایر زمان ها از سری های زمانی) بر روی مقادیر قبلی شان انجام خواهیم داد. جالبترین بخش تحقیق در مقاله بعدی انجام خواهد شد.

# calculate joinplot between real and predicted returns
def hourly_signals_statistics(symbol, lag,  hour, hour2, rfilter):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
# price differences for every hour series   
    H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True).diff(lag).dropna()
    H2 = rates.drop(rates.index[~rates.index.hour.isin([hour2])]).reset_index(drop=True).diff(lag).dropna()
# current returns for both hours    
    HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True)     
# previous returns for both hours    
    HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True)  
    
# Basic equation:  ret[-1] = ret[0] - (ret[lag] - ret[lag-1])
# or Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1])) 
    predicted = HF-(HF2-HL2)
    real = HL 
# correlation joinplot between two series    
    outcorr = pd.DataFrame()
    outcorr['Hour ' + str(hour)] = H['close']
    outcorr['Hour ' + str(hour2)] = H2['close']
# real VS predicted prices     
    out = pd.DataFrame()
    out['real'] = real['close']
    out['predicted'] = predicted['close']
    out = out.loc[((out['predicted'] >= rfilter) | (out['predicted'] <=- rfilter))]
# plptting results    
    from scipy import stats
    sns.jointplot(x='Hour ' + str(hour), y='Hour ' + str(hour2), data=outcorr, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) 
    sns.jointplot(x='real', y='predicted', data=out, kind="reg", height=7, ratio=6).annotate(stats.pearsonr)
hourly_signals_statistics('EURUSD', lag=25, hour=13, hour2=14, rfilter=0.00)

در اینجا توضیحی درباره موارد فوق الذکر داده می شود. دو سری به وسیله حذف ساعت های غیر لازم و براساس اینکه چه افزایش قیمتی (اختلاف آنها) محاسبه می شود، تشکیل می شوند. ساعات سری ها در پارامترهای “hour” و “hour2” معین شده اند. سپس توالی هایی با تاخیر 1 برای هر ساعت به دست می آوریم، یعنی سری های HF با یک ارزش جلوتر از HL می باشند. این امر محاسبه افزایش واقعی و افزایش پیش بینی شده، به همراه تفاوت بینشان، را انجام می دهد. در ابتدا، یک نمودار توزیعی برای افزایش ساعات اول و دوم می سازیم:

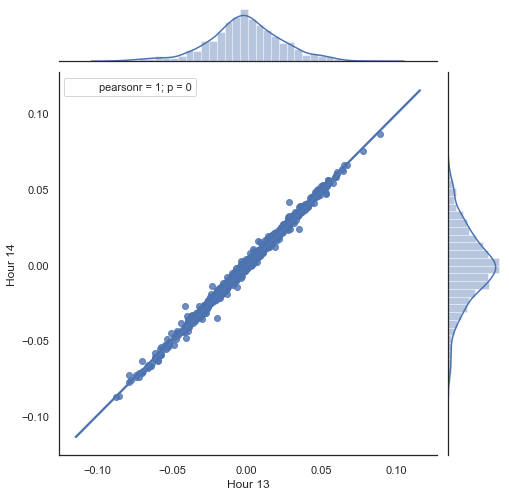
همانطورکه انتظار می رفت، افزایش ها شدیدا بهم وابسته هستند. حال به پیش بینی افزایش بعدی براساس افزایش قبلی می پردازیم. بدین منظور، در اینجا یک فرمول ساده وجود دارد که می تواند مقدار بعدی را پیش بینی کند:

Basic equation:  ret[-1] = ret[0] – (ret[lag] – ret[lag-1])

or Close[-1] = (Close[0]-Close[lag]) – ((Close[lag]-Close[lag*2]) – (Close[lag-1]-Close[lag*2-1])) 

پیش بینی با استفاده از اختلاف

در اینجا توضیحی از فرمول نتیجه وجود دارد. به منظور پیش بینی افزایش آینده، بر روی خط صفر می باشیم. مقدار افزایش بعدی ret[-1] را پیش بینی کنید. برای این کار، اختلاف بین افزایش قبلی (lag) و افزایش بعدی (lag-1) را از افزایش کنونی تفریق کنید. اگر همبستگی افزایش های بین دو ساعت مجاور شدید باشد، می توان انتظار داشت که افزایش پیش بینی شده با این معادله توضیح داده خواهد شد. در زیر توصیفی از معادله برای قیمت های نزدیک به هم می باشد. بنابراین، پیش بینی آینده بر اساس سه افزایش می باشد. دومین قسمت کد افزایش های آینده را پیش بینی و آنها را با مقادیر واقعی شان مقایسه می کند. نمودار آن عبارت است از:

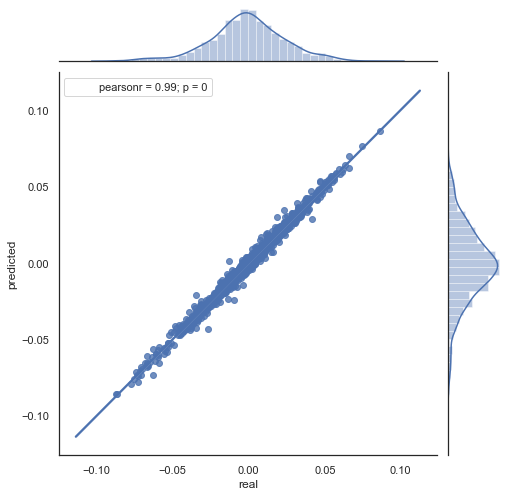
می توانید ببینید که نمودارهای اشکال 5 و 6 مشابه هم هستند. این دان معنی است که روش تعیین الگوها از طریق هم بستگی کافی می باشد. به همان صورت که مقادیر در نمودار توزیع شده اند؛ بر روی همان خط قرار نگرفته اند. این از خطاهای پیش بینی می باشد که تاثیر منفی بر روی پیش بینی دارند. می بایست به صورت جداگانه رسیدگی شوند (که خارج از اهداف این مقاله است). پیش بینی در حدود صفر واقعا جالب نیست: اگر پیش بینی افزایش قیمت بعدی برابر با مقدار کنونی باشد، نمی توانید سودی از آن به دست آورید. پیش بینی ها می توانند با استفاده از پارامتر rfilter فیلتر شوند.

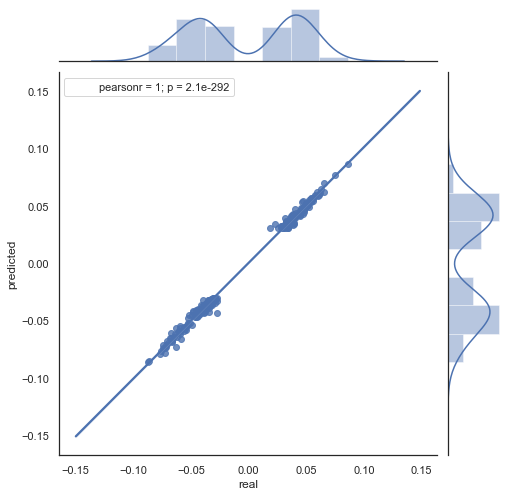
توجه داشته باشید که نقشه حرارتی با استفاده از داده های سال 2015 تا حال حاضر ساخته شده است. حال نقطه شروع را تا سال 2000 عقب ببریم:

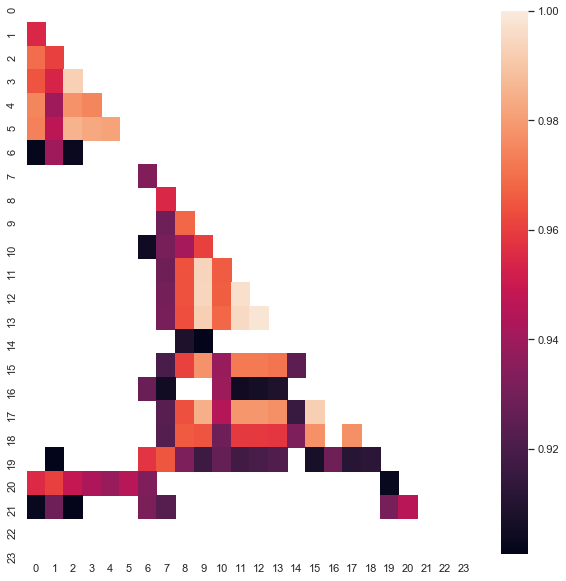
وابستگی نقشه حرارتی به زمان

همان طور که می توانید ببینید، نقشه حرارتی تا حدودی باریک تر است در حالی که وابستگی بین ساعات 13 و 14 کاهش یافته است. در همان زمان، مقدار متوسط افزایش مثبت است که اولویت بیشتری برای خرید ارائه می دهد. یک تغییر در مقدار متوسط بطور موثری تجارت در هر دو بازه زمانی را اجازه نمی دهد، پس شما باید انتخاب کنید.

اکنون به نمودار توزیعی حاصل در این بازه زمانی نگاه کنید (در اینجا فقط نمودار واقعی/پیش بینی را تهیه کرده ام):

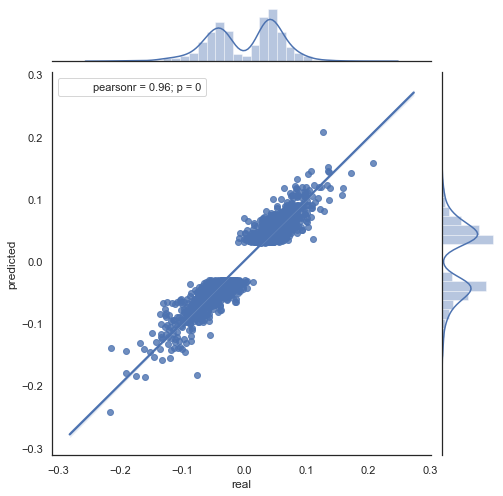
پراکندگی مقادیر افزایش یافته است که یک نقطه ضعف برای چنین بازه طولانی می باشد.

بنابراین یک فرمول و یک نظریه تقریبی برای توزیع افزایش های واقعی و پیش بینی شده در برخی از ساعت ها به دست آورده ایم. به منظور شفافیت بیشتر، وابستگی ها می توانند به صورت سه بعدی نمایش داده شوند.

# calculate joinplot between real an predicted returns
def hourly_signals_statistics3D(symbol, lag,  hour, hour2, rfilter):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
    rates = pd.DataFrame(rates['close'].diff(lag)).dropna()
    
    out = pd.DataFrame();
    for i in range(hour, hour2):
        H = None; H2 = None; HF = None; HL = None; HF2 = None; HL2 = None; predicted = None; real = None;
        H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True)
        H2 = rates.drop(rates.index[~rates.index.hour.isin([i+1])]).reset_index(drop=True)
        HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True);     # current hours
        HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True)  # last day hours
    
        predicted = HF-(HF2-HL2)
        real = HL 
    
        out3D = pd.DataFrame()
        out3D['real'] = real['close']
        out3D['predicted'] = predicted['close']
        out3D['predictedABS'] = predicted['close'].abs()
        out3D['hour'] = i
        out3D = out3D.loc[((out3D['predicted'] >= rfilter) | (out3D['predicted'] <=- rfilter))]
        
        out = out.append(out3D)
        
    import plotly.express as px
    fig = px.scatter_3d(out, x='hour', y='predicted', z='real', size='predictedABS', color='hour', height=1000, width=1000)
    fig.show()
hourly_signals_statistics3D('EURUSD', lag=24, hour=10, hour2=23, rfilter=0.000)

این تابع از فرمول شناخته شده قبلی برای محاسبه مقادیر واقعی و پیش بینی شده استفاده می کند. هر نمودار توزیعی مجزا وابستگی واقعی/پیش بینی  برای هر ساعت را نشان می دهد به گونه ای که یک سیگنال در افزایش ساعت 100 در روز قبل تولید شد. ساعات 10 تا 23 به عنوان مثال استفاده می شوند. همبستگی بین نزدیکترین ساعات ماکزیمم است. وقتی فاصله افزایش یابد، همبستگی کاسته می شود (نمودارهای توزیعی بیشتر شبیه دایره می شوند). با شروع از ساعت 16، ساعات بعدی وابستگی کمی به ساعت 10 در روز قبل دارند. با استفاده از ضمیمه، می توانید نمای سه بعدی را چرخانده و برش هایی را جهت کسب اطلاعات دقیق تر انتخاب کنید.

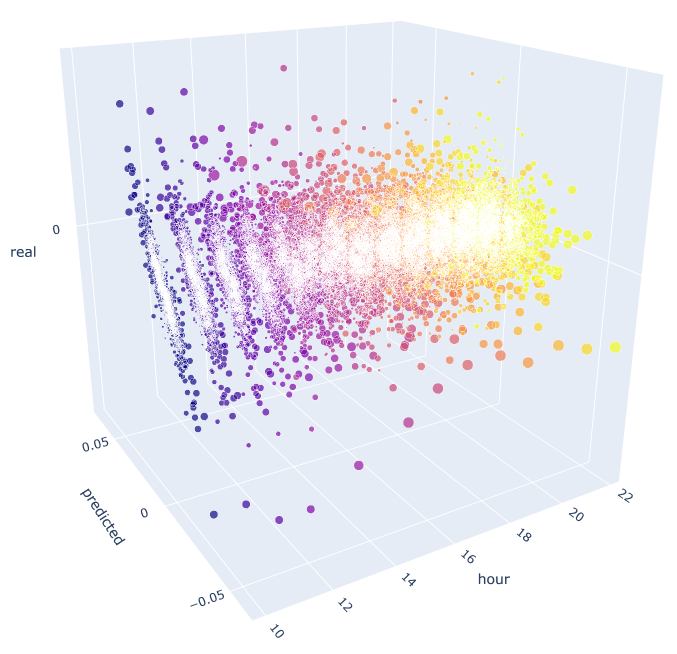
اکنون زمان آن است که یک راهنمای حرفه ای بسازید تا ببینید چگونه عمل می کند.

مثالی از راهنمای حرفه ای تجاری الگوهای فصلی معین

مشابه مثالی از مقاله قبلی، ربات در یک الگوی فصلی تجارت می کند که فقط بر اساس رابطه آماری بین افزایش کنونی و قبلی اش در یک ساعت معین می باشد. با این تفاوت که در ساعات دیگر تجارت انجام می شود و از یک قاعده بر اساس فرمول ارائه شده استفاده می شود.

حال یک مثال با استفاده از فرمول حاصل برای تجارت، بر اساس مطالعه آماری، در نظر بگیریم:

input int OpenThreshold = 30;     //Open threshold
input int OpenThreshold1 = 30;    //Open threshold 1
input int OpenThreshold2 = 30;    //Open threshold 2
input int OpenThreshold3 = 30;    //Open threshold 3
input int OpenThreshold4 = 30;    //Open threshold 4
input int Lag = 10;
input int stoploss = 150;         //Stop loss
input int OrderMagic = 666;       //Orders magic
input double   MaximumRisk=0.01;  //Maximum risk
input double   CustomLot=0;       //Custom lot

The following interval with patterns was determined: {10, 11, 12, 13, 14}. Based o

فواصل زیر با الگوها معین می شوند:{10، 11، 12، 13، 14}. بر این اساس، پارامتر “آستانه ورودی” (Open threshold) می تواند برای هر ساعت به صورت منفرد تنظیم شود. این پارامترها مشابه rfilter در شکل 9 می باشند. متغیر lag حاوی مقدار تاخیر برای افزایش ها می باشند ( به خاطر داشته باشید که ما به صورت پیش فرض تاخیر 25 را آنالیز نمودیم، یعنی تقریبا یک روز برای محدوده زمانی H1). تاخیرها می توانند بطور جداگانه برای هر ساعت تنظیم شوند، اما در اینجا از یک مقدار مشابه برای تمامی ساعات جهت ساده سازی استفاده می شود. توقف ضرر نیز برای تمام موقعیت ها یکسان است.تمامی این پارامترها می توانند بهینه سازی شوند.

تابع منطقی تجاری به شرح زیر می باشد:

void OnTick() {
//---
   if(!isNewBar()) return;
   CopyClose(NULL, 0, 0, Lag*2+1, prArr);
   ArraySetAsSeries(prArr, true);
   const double pr = (prArr[1] - prArr[Lag]) - ((prArr[Lag] - prArr[Lag*2]) - (prArr[Lag-1] - prArr[Lag*2-1]));
   TimeToStruct(TimeCurrent(), hours);
   if(hours.hour >=10 && hours.hour <=14) {
      //if(countOrders(0)==0)
      //   if(pr >= signal && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY))
      //      OrderSend(Symbol(),OP_BUY,LotsOptimized(), Ask,0,Bid-stoploss*_Point,NormalizeDouble(Ask + signal, _Digits),NULL,OrderMagic,INT_MIN);
      if(CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_SELL)) {
         if(pr <= -signal && hours.hour==10)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal, _Digits),NULL,OrderMagic);
         if(pr <= -signal1 && hours.hour==11)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal1, _Digits),NULL,OrderMagic);
         if(pr <= -signal2 && hours.hour==12)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal2, _Digits),NULL,OrderMagic);
         if(pr <= -signal3 && hours.hour==13)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal3, _Digits),NULL,OrderMagic);
         if(pr <= -signal4 && hours.hour==14)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal4, _Digits),NULL,OrderMagic);
      }
   }
}

محاسبه افزایش قیمت در زبان ام کیو ال با استفاده از فرمول pr

ثابت pr توسط فرمول مشخص بالا محاسبه می شود. این فرمول افزایش قیمت را در خط بعدی پیش بینی می کند. سپس شرایط هر ساعت بررسی می شود. اگر افزایش مطابق با آستانه حداقل یک زمان ویژه باشد، معامله فروش باز می شود. قبلا دریافتیم که انتقال افزایش متوسط به بازه منفی خرید های را در فواصل 2015 تا 2020 بی تاثیر می کند. می توانید خودتان این مسئله را بررسی نمایید.

اکنون بهینه سازی ژنتیکی برای پارامترهای مشخص در شکل 11 را اجرا و نتیجه را مشاهده می نماییم:

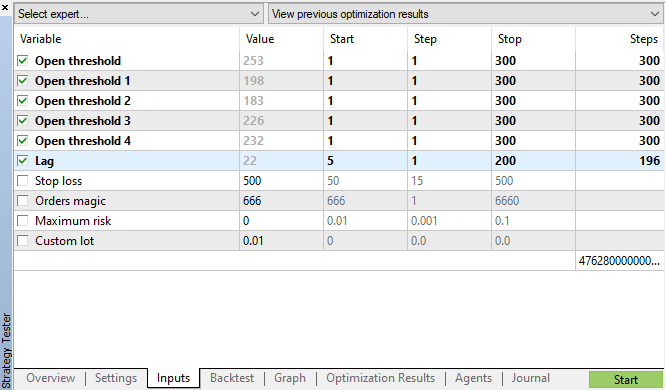
حالی به نمودار بهینه سازی نگاه کنید. در فواصل بهینه شده، موثرترین مقادیر تاخیر بین ساعات 17 تا 30 قرار دارند که خیلی به فرض ما درباره وابستگی افزایش های یک ساعت مشخص در روز کنونی با همان ساعت در روز قبل نزدیک است:

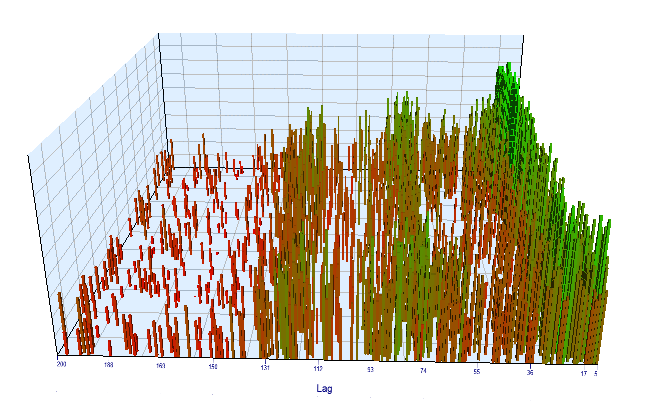
نمودار پیشرو هم مشابه به نظر می رسد:

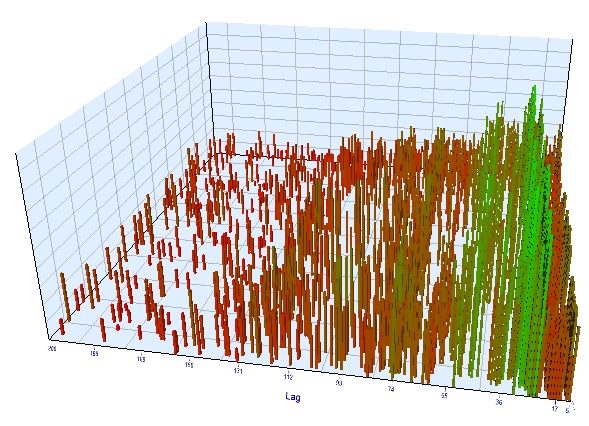
در اینجا بهترین نتایج پیش آزمون و جداول بهینه سازی پیشرو ارائه می شود:

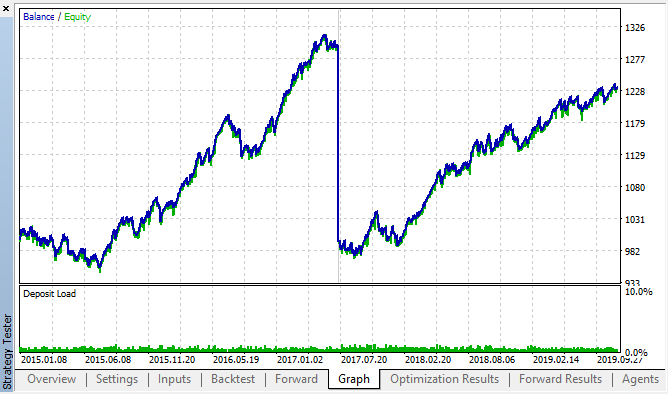
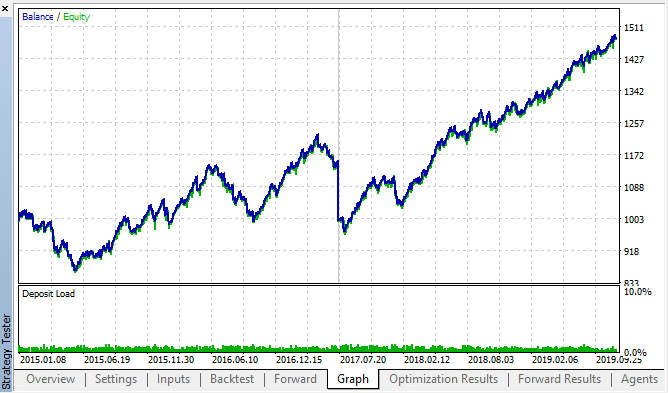
قابل رویت است که الگو در سراسر بازه زمانی 2015 تا 2020 ادامه دارد. میتوانیم فرض نماییم که نظریه اکونومتری کاملا خوب عمل می کند. وابستگی هایی بین افزایش در ساعات مشابه روزهای بعد هفته، به همراه چند دسته بندی، وجود دارد (وابستگی ممکن است با همان ساعت نباشد اما با ساعت مجاور خواهد بود). در مقاله بعدی، تحلیل خواهیم کرد که چگونه از الگوی دوم استفاده نماییم.

بیشتر بخوانید : نحوه اتصال توییتر از طریق ام کیو ال

بررسی دوره افزایش بر روی یک بازه زمانی دیگر

اجازه دهید تا بررسی دیگری بر روی بازه زمانی M15 انجام دهیم. فرض کنیم به دنبال همبستگی مشابه بین ساعت کنونی و همان ساعت در روز قبل می باشیم.در این مورد تاخیر موثر می بایست 4 برابر بزرگتر و در حدود 96=4*24 باشد برای اینکه هر ساعت حاوی دوره های M15 می باشد. اینجانب راهنمای حرفه ای را با همان تنظیمات مشابه و با بازه زمانی M15 بهینه سازی نموده ام.

در فواصل بهینه سازی شده، تاخیر موثر حاصل از 60 کوچکتر است که عجیب می باشد. شاید بهینه ساز الگوی دیگری پیدا کرده است یا اینکه EA بیش از اندازه بهینه شده است.

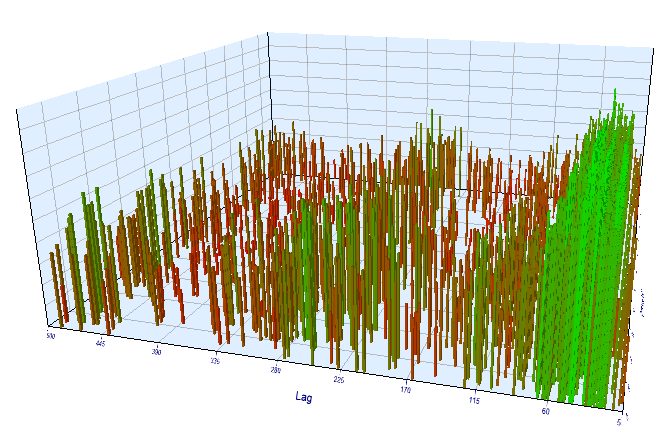
همانند نتایج آزمون پیشرو، تاخیر موثر نرمال و مطابق با 100 است که الگو را تایید می نماید:

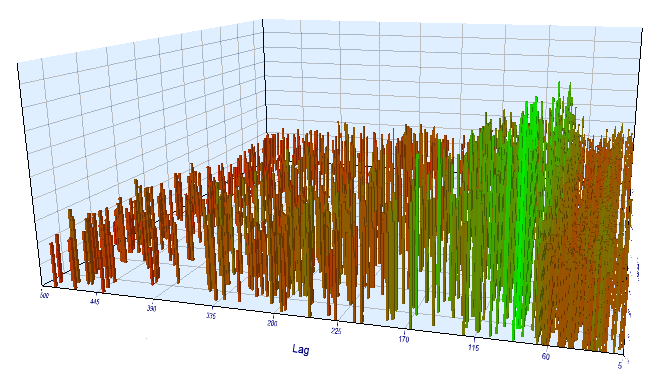
اجازه دهید تا بهترین نتایج پیشرو و پیش آزمون را مشاهده کنیم:

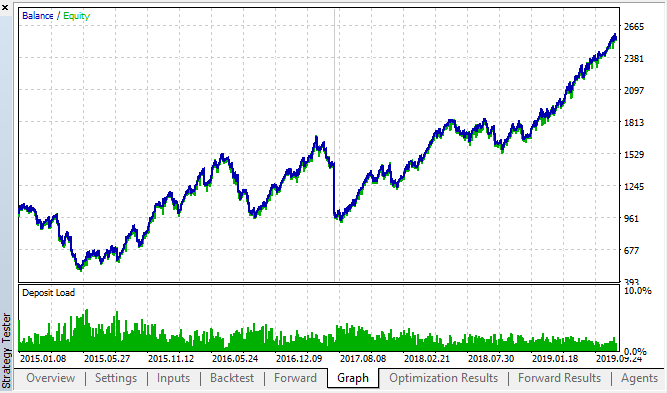
منحنی حاصل مشابه نمودار منحنی H1 و با یک افزایش مشهود در تعداد معاملات می باشد. شاید این استراتژی قابل بهینه شدن برای بازه های زمانی کوچکتر باشد.

پیشنهاد می کنیم اگر به دنیال یادگیری این نسخه از زبان ام کیو ال هستید، حتما به آموزش زبان MQL5 در آکادمی ایران ام کیو ال مراجعه کنید.

نتیجه گیری

در این مقاله، عبارت زیر را مطرح کردیم:

همبستگی افزایش قیمت به وجود الگوهای فصلی، به اندازه افزایش های کوتاه مدت، وابسته است.

اولین بخش کاملا تایید شد: همبستگی بین افزایش های ساعتی از هفته های مختلف وجود دارد. عبارت دوم تلویحا اثبات شد: همبستگی دسته بندی دارد که بدین معنی است که افزایش های ساعتی نیز وابسته به افزایش های مجاور خود می باشند.

لطفا توجه داشته باشید که راهنمای حرفه ای ارائه شده، بدون هیچ دلیلی، تنها متغیر ممکن برای معامله همبستگی های یافته شده می باشد. تابع منطقی ارائه شده دیدگاه نویسنده را بر روی همبستگی ها منعکس می کند در حالی که بهینه سازی های EA انجام گردید تا الگوهای یافته شده از طریق تحقیقات آماری را بیشتر تایید نماید.

از آنجاییکه بخش دوم مطالعه ما به تحقیقات قابل توجه بیشتری نیاز دارد، از یک دستگاه ساده مدل آموزشی در مقاله بعدی استفاده می کنیم تا کاملا بخش دوم عبارت را تایید یا تکذیب نماییم.

ضمیمه حاوی چهارچوب کاری آماده به استفاده در قالب Jupyter notebook می باشد که می توانید برای ابزارهای مالی دیگر از آن استفاده نمایید. نتایج می توانند بعدا با استفاده از آزمون متصل به EA آزموده شوند.

این مقاله ترجمه شده توسط تیم آکادمی ایران ام کیو ال می باشد. 

صفحه اصلی مقاله