وقتی که هیچ کامپیوتری نبود و کالاهای واقعی در بازارهای واقعی معامله می شدند، روش کلاسیک ارائه سری های قیمت به عنوان فواصل زمانی  (بازه زمانی) خیلی وقت پیش، در آغاز تشکیل بازارهای مالی، ظاهر شدند. ذخیره سازی هر تغییر قیمت در طول روز مشکل بود. علاوه بر این، بی فایده بود زیرا قیمت های به سرعت تغییر نمی کردند. بنابراین، راه حل مشخص ثبت مقادیر قیمت در یک فاصله زمانی معمول، بود. به نظر منطقی است: امروز گندم 90 سنت است در حالی که دیروز 80 سنت بود. همه چیز واضح است: تقاضا افزایش یافته و قیمت بالا رفته است. معاملات زیادی، در مقایسه با معاملات بازار امروز، وجود نداشتند به همین خاطر قیمت ها به ندرت تعیین مجدد می شدند.با ظهور و پیشرفت تحلیل داده قیمت ها، با هدف اینکه کدام یک پیش بینی بهتری از رفتار قیمت داشت، و با افزایش تعداد انجام معاملات، برای مردم مهم شد که دریابند کدام بالاترین و پایین ترین قیمت برای برخی از دوره های زمانی بودند. بدین ترتیب، اطلاعات درباره قیمت 80 سنت دیروز و قیمت 90 سنت امروز دیگر کافی نبود. همه می خواستند بدانند که بالاترین و پایین ترین قیمت در یک دوره زمانی خاص چه بود. این امر موجب شد تا نمودارهای کندل استیک و میله ای اختراع شدند.همانطور که انجام معاملات افزایش یافت، گسسته سازی بازار مالی سری های قیمت دقیق تر و دقیق تر شد. اکنون، ما از قبل گسسته سازی بازار مالی دقیقه ای یا حتی بازه های کوچکتر، مانند ثانیه و 10 ثانیه، را به کار بردیم.

 

فواید اصلی گسسته سازی بازار مالی سری های قیمت

• راحتی. ما دقیقا می فهمیم که میله بعدی در یک دقیقه بعد شکل خواهد گرفت و مقادیر قیمت آغاز، پایان، بالا و پایین دریافت خواهیم کرد.
• کارایی منابع. ارائه کندل استیک فقط اجازه ذخیره 4 عدد در دوره زمانی را می دهد اگر که دقت بیشتری لازم نباشد. اگر هر تغییری در مزایده، قیمت درخواستی و نهایی، را ذخیره کنید، حجم تاریخچه یک ساله خیلی زیاد، در حدود چند گیگابایت، خواهد بود. اگر نیاز به دانلود و ذخیره تاریخچه 10 یا 20 ساله، نه برای یکی بلکه برای 200 تا 500 نماد، داشته باشید، این امر واقعا مشکل خواهد بود. علاوه بر این، منابع کامپیوتری عظیمی برای پردازش گیگابایت های تاریخچه نیاز خواهد بود. برای همین است که تحلیل و پردازش کندل استیک جالب تر به نظر می رسد.
• مقیاس بندی آسان و تحلیل بصری. هر گاه لازم به دیدن تصویر کلی تری باشد، مقیاس گسسته سازی می تواند به هفته ها و ماه ها گسترش یابد و صفحه نمایش داده ها را برای هر تعداد سالی که نیاز باشد، نشان خواهد داد. اگر دقت بیشتری لازم باشد، می توانید مقیاس نمایش را به آنچه در یک دقیقه اتفاق می افتد، کاهش دهید.
• خطی بودن در زمان. شاید ساده ترین چیز در این مقاله این است که هر تاریخچه سالانه به صورت بصری در همان فضای نمایشی ایجاد شود. یافتن نموداری از سال یا ساعت قبل آسان و شهودی است. در ابتدا، خطی بودن در زمان به نظر می رسد که پارامتر خیلی مهمی باشد اما زمان هایی است که تصمیم های درست غیرعقلانی می باشد.
• راحتی مقایسه قیمت برای چندین ابزار.
• خصوصیات گسسته سازی سیگنال

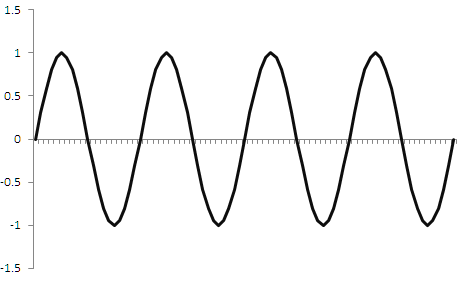
داده های گسسته سازی بازار مالی نه تنها در معاملات، بلکه در زمینه های دیگری از پردازش سیگنال لازم است. به عنوان مثال، در موسیقی سیگنال عموما پیوسته ای دیجیتالی می شود. به وسیله گسسته سازی زمان کدگذاری می شود. سیگنال مقدار را در فواصل زمانی خاصی که در حافظه نوشته شده است، افزایش می دهد. این سیگنال می تواند مجددا با استفاده از بعضی از دستکاری ها به سیگنال پیوسته تبدیل شوند. گسسته سازی بازار مالی سیگنال پیوسته یک مبحث مطالعه شده است. به عنوان مثال، قوانینی که از تئوری kotelnikov (Nyquist-Shannon) تبعیت می کنند، بیان می دارند: یک سیگنال می تواند کاملا ذخیره شود اگر فرکانس گسسته سازی 2 برابر یا بیشتر از فرکانس سیگنال باشد. بنابراین، اگر فرکانس سیگنال 1 هرتز باشد، در نتیجه مقدار افزایش آن باید حداقل بیشتر از 2 بار در ثانیه خوانده شود (یعنی با فرکانس 2 هرتز). فقط در این مورد دستیابی به شکل اصلی اش بعد از گسسته سازی ممکن خواهد بود. شکل 1 نشان می دهد که چه اتفاقی می افتد اگر موج سیگنال 1 هرتزی را با نرخ نمونه ای 2 هرتز گسسته سازی نماییم. سیگنال به رنگ سبز می باشد و نتیجه گسسته سازی بازار مالی به رنگ قرمز نشان داده شده است.

شکل 1

 

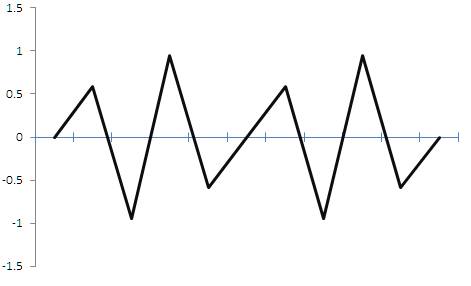
بعد از گسسته سازی بازار مالی، موج سینوسی به شکل موج مثلثی تبدیل می شود. البته چندین خطا وجود دارد، اما این سیگنال مثلثی        می تواند مجددا توسط فیلتر های پایین گذر به سینوسی تبدیل شوند. یعنی اینکه می توانیم یک سیگنال را با حفظ ایده، پریود و دامنه اش، هرچند با مقداری خطا، ذخیره کنیم. چنین تحریفاتی در موسیقی بحرانی در نظر گرفته می شود اما برای معاملات آنقدر مهم نیستند. اما چه اتفاقی می افتد اگر نرخ گسسته سازی کمتر از نرخ سیگنال اصلی باشد؟ یک نمونه در شکل 2 زیر نشان داده شده است.

شکل 2

 

شکل نشان می دهد که اگر فرکانس گسسته سازی بازار مالی کمتر از دو برابر فرکانس سیگنال باشد، سیگنال حاصل به طور شگرفی انحراف دارد و عملا یک سیگنال اتفاقی دریافت خواهیم کرد که هیچ ربطی به سیگنال اصلی ندارد. وقتی چنین چیزی در معاملات اعمال شود، اول اجازه فروش به ما می دهد وقتی دامنه بالا را پیدا کنیم و اجازه خرید می دهد وقتی دامنه پایین را ببینیم. همچنین، در این مورد فرکانس را می دانیم. بعد از گسسته سازی اشتباه، اطلاعات مربوط به دامنه و فرکانس سیگنال را از دست می دهیم. یک سگنال دوره ای قطعی با خصوصیات معلوم به یک سیگنال غیر دوره ای تصادفی با خصوصیات نامعلوم، به دلیل انتخاب نرخ گسسته سازی اشتباه، تبدیل می شود.

دو سوال منطقی از دانش بالا پیش می آید: آیا اشتباه می کنیم که سری های قیمت را گسسته سازی می نماییم؟ و آیا سری های قیمت یک سیگنال گسسته یا پیوسته است و چه پارامترهایی دارد؟

پاسخ ساده نیست و در عین حال خیلی مهم است.

آیا سری های قیمت گسسته یا پیوسته اند؟

اگر مکانیزم تشکیل قیمت بازار را بدانیم، سوال قابل پاسخ دهی می باشد. وارد جزئیات نمی شوم زیرا توضیحات در مقاله اصول تبادل قیمت از طریق نمونه تبادل مسکو بازار مشتقات فراهم شده است. بعضی از حاضرین سفارشات را در عمق بازار قرار می دهند و بقیه مقدار لازم را در قیمت لازم خریداری می کنند. این چیزی است که هنگام تشکیل نمودار قیمت اتفاق می افتد. سطوح گسسته اند یعنی ممکن است یک سفارش در قیمت 1، 2، 3 و الی آخر، با کمی دقت، قرار بیگیرد. حجم تنظیم شده در مزایدات و خرید شده توسط خریداران نیز گسسته است زیرا می توانید 1، 2، 3 و واحد بیشتر خریداری کنید. شکل 3 زیر نمونه ای از عمق بازار را نشان می دهد؛ می توانید ببینید که قیمت ها و حجم ها مقادیر گسسته دارند.

شکل 3

در نتیجه، می توانیم نتیجه گیری کنیم که سری های قیمت ذاتا گسسته است. قیمت در راستای سطوح گسسته منتقل می شود بعد از اینکه معامله گران مقدار حجم گسسته را خریداری می کنند.

 

عملکرد اینکه قیمت در گسسته سازی بازار مالی چند است؟

دریافتیم که خود سری های قیمت گسسته است اما عملکرد کدام پارامتر، تغییر قیمت است؟

گسسته سازی سیگنال صدا در فواصل معمولی یک راه حل مقبول است زیرا سیگنال صدا تابعی است که در طول زمان تغییر می کند. خود سیگنال دامنه ای است که وابسته به زمان است. این خصوصیت سیگنال اساسی است. به همین خاطر است که در اینجا مشکلی پیش نمی آید.

سری های قیمت طبیعت متفاوتی دارد. در این جا دامنه (قیمت) در طول زمان تغییر می کند اما زمان دلیل تغییر قیمت نیست. اگر سعی در فهم دلیل تغییر قیمت دارید، پس سوال به این راحتی نیست. چندین فرضیه می تواند باشد:

1. قیمت به عنوان تابعی از معاملات. قیمت مطابق با معاملات انجام شده تغییر می کند زیرا انجام معاملات قیمت را حرکت می دهد. اما انجام معاملات شاید به تغییر قیمت منتهی نشود. به عنوان مثال، 10 سهم با قیمت 1 دلار موجود است. یک معامله گر 4 سهم خریداری می کند و 6 سهم در همان قیمت باقی می ماند. بنابراین، انجام معامله صورت گرفته است ولی قیمت تغییر نکرده است. با این وجود، این کار حجم موجود به این قیمت را کاهش داده است که می تواند منجر به تغییر قیمت بعدی شود وقتی که معامله گر بعدی تمام سهم را بخرد. قیمت ها فقط زمانی تغییر می کنند که تعداد سهم های با 1 دلار برای پوشش تقاضا کافی نبوده و تمام مقادیر موجود خریداری شود. در این مورد، قیمت درخواستی به 1.1 دلار حرکت می کند. با این وجود، سایر معامله گران کماکان قادر به سفارش با قیمت 1 دلار هستند و قیمت درخواستی را بر می گردانند.
2. قیمت به عنوان تابعی از تمام انجام معاملات در بازار. قیمت می تواند نه تنها هنگامی که معامله گران کلیه حجم را در سطح خاصی خرید کردند تغییر کند، بلکه وقتی به سادگی سفارشات خود را کنسل می کنند یا به سطح دیگری ببرند، نیز تغییر کند. بنابراین، هیچ معامله ای انجام نشده است ولی قیمت درخواستی و مزایده حرکت خواهد کرد.
3. قیمت به عنوان تابعی از سود. قیمت می تواند تغییر کند زیرا معامله گران مقدار ارزیابی خودشان را مجددا تعیین نمایند. کاملا می تواند دلایل مختلفی برای تعیین مجدد ارزش وجود داشته باشد. در هر موردی، تعیین مجدد ارزش خیلی نزدیک به سود معامله گران است. در تئوری، قیمت گذاشته شده سودده ترین قیمت برای کل مجموعه معامله گران، شمال خریداران و فروشندگان می باشد (حتی اگر این سود منفی باشد). بازار اصولا برای سودهای حداکثر و تعیین قیمت تعادلی بهینه مورد قبول برای خریدار و فروشنده ساخته شده است. این سود شاید مرتبط با بعضی از درخواست ها نباشد. به عنوان مثال، یک تنخواه سرمایه نیاز دارد تا فورا یک دارایی را بفروشد. آنها حاضرند تا این کار را انجام دهند حتی اگر ضرر بدهند زیرا ممکن است مقداری سود دیگر با انجام این عمل به دست آورند، مثلا قادر به خرید دارایی دیگری بوده یا سود را با متقاضیانشان تقسیم کنند. طبیعت سود می تواند متفاوت باشد. در چنین موردی، قیمت تابعی از هر تعیین مجدد سود برای هر معامله گر می باشد.
4. قیمت به عنوان تابعی از خود. به وضوح، هر تغییر قیمتی منجر به تغییر در سودهای معامله گران بازار می شود. سودها می توانند بدون تغییر قیمت تغییر کنند اما وقتی قیمت تغییر می یابد، سود معامله گران تغییر خواهد کرد. این امر تعریف دقیقی از تغییر قیمت نیست اما این اجازه را به می دهد تا تقریبا به یک مدل ایده آل نزدیک شویم و چندین فرضیه بسازیم که تاثیر زیادی بر نتایج آینده نداشته باشد. ما اساسا تغییرات قیمت را معامله می کنیم. حتی اگر استراتژی سود سهام را انتخاب کنیم (قیمت را در نظر نگیریم)، پرداخت سود سهام نهایتا منجر به تغییر قیمت خواهد شد. در این مورد، تغییر قیمت سیگنالی برای شیفت نمودار به سمت چپ است. قیمت ثبتی فقط زمانی تغییر می یابد که به یک نقطه حرکت کند. هر مرحله می تواند بر اساس مقیاس ترجیحی استفاده شود: ارزش قیمتی می تواند هر زمین که n نقطه بالا یا پایین برود، ثبت شود.

اینجانب فرض می کنم گزینه سوم محتمل تر باشد که قیمت را تابعی از تعیین مجدد سود بیان می کند. اما غیر ممکن است که سود هر معامله گر را محاسبه نمود تا اینکه سری ها را گسسته سازی نمود. در دو مورد اول، ممکن است انجام معاملات تجاری و غیرتجاری در بازار ارز محاسبه شود اما همچنین می تواند مشکلاتی به همراه داشته باشد. به عنوان مثال، یک دارایی می تواند در دو یا چند تبادل مختلف معامله شود. یا اگر مشتقات یک دارایی، مانند آینده یا گزینه ها، وجود داشته باشد، آیا نیاز داریم که انجام معاملاتی را که به طور غیرمستقیم مرتبط با دارایی است، محاسبه کنیم؟ این سوالات نیازمند مطالعه وسیع و مجزایی می باشد. در هر مورد، تمام چهار مورد به طور غیرمستقیم به یکدیگر مرتبطند. گزینه چهارم، که قیمت تابعی از خودش می باشد، اجازه تحقیقات بعدی می دهد و موجب می شود که فرض کنیم این یک مدل تقریبی می باشد.

نرخ تغییر در قیمت دارایی بر اساس تعداد معاملات است. انجام معاملات بیشتر، تغییر مداوم تر قیمت را منجر می شود که به معنی وجود همبستگی مستقیم است. به همین ترتیب، اگر معامله گران زیادی در بازار باشند، تعداد معاملات زیادی انجام می شود که منجر به تعداد معاملات بیشتر شده و فرکانس قیمت دارایی بالا خواهد بود.

 

خصوصیات گسسته سازی بازار مالی سری های قیمت به وسیله فواصل زمانی و مولفه تصادفی

مطابق با مدل تقریبی ما، قیمت تابعی از خودش می باشد و ما قیمت را فقط هنگامی که تا چند تعداد نقطه تغییر می کند، گسسته سازی می نماییم حتی اگر کاملا صحیح نباشد، این فرض فهم بعدی موضوع بدون تاثیر بر نتیجه نهایی را میسر می سازد. علاوه بر این، برای سوددهی می بایست بدانیم که قیمت تغییر کرده است. به علاوه، می بایست بدانیم که چگونه تغییر نموده است تا به جستجوی الگوها بگردیم.

هر تغییر قیمت یک نقطه ای (در اینجا نقطه کوچکترین تغییر قیمت ممکن است) برابر با یک مرحله خواهد بود. حال ببینیم که چه اتفاقی می افتد وقتی که چنین مجموعه ای بر اساس زمان گسسته سازی می شود. به وضوح، تعداد نقاطی که قیمت در واحد زمان از آنها عبور می کند وابسته به فعالیت معاملات می باشد. هر چه فعالیت معاملات (تعداد معاملات انجام شده) بیشتر باشد، قیمت از مراحل بیشتری عبور می کند. فعالیت معاملات مستقیما به حرکت قیمت ربط ندارد اما حرکت قیمت به فعالیت معاملات بستگش دارد: هر چه فعالیت بیشتر باشد، حرکت قیمت بیشتر خواهد بود. وابستگی غیرمستقیم است اما همبستگی مثبت می باشد. فرض کنید 1 مرحله برابر با 10 نقطه باشد. کندل استیک یک ساعته برای نمونه استفاده خواهد شد. دو شکل زیر قیمت ها را به شکل بلوک نشان می دهد. بلوک ها مشابه میله های رنکو است اما بر طبق اصول کمی متفاوت ساخته می شوند. از بالا و پایین کندل استیک های کلاسیک استفاده می کنند که بالاترین و پایین ترین ارزش قیمتی را برای زمان تشکیل بلوک نشان می دهد. همانند کندل استیک ها، بلوک ها 4 خصوصیت دارند: آغاز، بالا، پایین و پایان. تفاوت آنها با کندل استیک در فاصله بین آغاز و پایان می باشد که همواره ثابت بوده و با نقاط بیان می شود. بلوک وقتی بسته می شود که قیمت به طور عمودی به میزان N نقطه عبور کند. به عنوان مثال، اندازه بلوک 10 نقطه است. هر گاه قیمت 10 نقطه عمودی حرکت کند، بلوک بسته شده و یک بلوک جدید شروع می شود.

شکل 4

 

اگر یک بلوک برابر با یک مرحله N نقطه ای باشد، پس ببینیم که درون یک کندل استیک یک ساعته چه اتفاقی می افتد. اشکال 4 حرکاتی را نشان   می دهد که در طول تشکیل کندل استیک یک ساعته اتفاق افتاده است. در شکل بالایی، قیمت در یک ساعت 10 بلوک عمودی را طی کرده است. اگر اندازه بلوک 10 نقطه باشد، پس اندازه کندل استیک 100 نقطه است. مجموعا، 25 بلوک در کل زمان تشکیل کندل استیک شکل گرفته است که برابر با 25 مرحله است. نمونه دیگر در شکل پایینی نشان داده شده است که در آن قیمت از 0 بلوک یا 0 نقطه در طول زمان تشکیل کندل استیک عبور می کند. در مجموع، قیمت از 40 بلوک، یا 40 مرحله، در طول زمان تشکیل بلوک عبور می کند. حال نموداری را مشاهده می کنیم که حاوی چنین کندل استیکی است. این نمودار در شکل 5 نشان داده شده است. کندل استیک هر یک ساعت بسته می شود و سری های قیمت مشخصا تابعی از زمان نیستند. در یک مورد ساده شده، تابعی از انجام معاملات می باشد که همبستگی مثبتی با تعداد نقاط عبوری دارد. از آنجاییکه نقاط را به بلوک ها تبدیل کرده ایم، تعداد بلوک ها همبستگی مثبتی با تعداد معاملات دارد. عملا، هر کندل استیک (با فرض یک ساعت) مشخص می شود که تعداد تصادفی از بلوک ها، یا مراحل N نقطه ای، داشته باشد. بعدا خواهیم دید که چرا این امر مهم است. این امر به دلیل آن است که کندل استیک به سادگی بعد از یک زمان معین بسته می شود علی رغم آنکه فرآیندها در بازار رخ می دهد. زمان یک پارامتر خارجی است که رابطه کمی با قیمت فرآیندهای مربوطه دارد. به عبارت دیگر، تغییرات قیمت به خاطر گذشت یک ساعت نیست بلکه به دلایل دیگری می باشد که یکی از آنها نیز می تواند زمان سپری شده باشد.

شکل 5

 

فعالیت معاملات می تواند به طور مشهودی در طول زمان تغییر کند. علاوه بر این، فعالیت معاملات ابزارهای معاملاتی مختلف، متفاوت از هم هستند. به علاوه، توسعه معاملات الگوریتمی منجر به افزایش تعداد معاملات در واحد زمان و بازدهی آن می شود، یعنی اینکه مقایسه مستقیم کندل استیک های بین 2010 تا 2020 اشتباه خواهد بود زیرا هرکدام از آنها حاوی تعداد متفاوتی از معاملات بودند.

حال یک ساده سازی دیگر انجام می دهیم و بازار را به سمت یک مدل گام تصادفی ببریم. البته، بازار یک گام تصادفی نیست اما با این روش فهم آن راحت تر خواهد شد. بعدا به بازارهای واقعی باز خواهیم گشت.

تئوری حد وسط بیان می دارد که جمع کثیری از متغیرهای تصادفی کم وابسته و دارای مقیاس های تقریبا مشابه (هیچکدام از آنها میزان مشارکت در جمع را تعیین نمی کنند) تقریبا به صورت نرمال توزیع می شود. همان طور که ما انجام داده ایم، می توانیم از این تئوری نتیجه بگیریم که به طور متوسط، فرآیند تصادفی ما فاصله N مرحله را طی می کند که به صورت عمودی تقریبا متناسب با ریشه دوم تعداد مراحل است. اگر یک بلوک یک مرحله باشد، پس برای 100 بلوک قیمت به صورت عمودی برابر با 100^0.5=10 بلوک خواهد بود. می تواند موارد ایزوله بیشتر یا کمتری وجود داشته باشد اما به طور متوسط، سریه های تصادفی از قانون توزیع نرمال تبعیت می کنند. تعداد مراحل این سری های تصادفی کمی وابسته به زمان خواهند بود زیرا مراحل توسط فعالیت قیمت تولید می شوند که در طول زمان می توانند خیلی تغییر کنند.

بنابراین، اندازه کندل استیک یک ساعته برای چنین سری های قیمت تصادفی به طور متوسط متناسب با N^0.5 خواهدبود که در آن N تعداد مراحل درون کندل استیک است. یعنی اینکه اندازه کندل استیک یک ساعته مطابق با قانون توزیع نرمال خواهد بود. بعدا با احتساب این واقعیت که تعدادی مراحل تصادفی می توانند درون یک کندل استیک وجود داشته باشند، می توانیم نتیجه بگیریم که اندازه کندل استیک نیز مطابق با قانون توزیع نرمال خواهد بود. یعنی اندازه کندل استیک برابر با ریشه دوم تعداد مراحل درون کندل استیک می باشد. این عبارات را بررسی می کنیم. بدین منظور از 50000 کندل استیک یک دقیقه ای GBPUSD برای بازه 18/05/2020 تا 03/07/2020 استفاده می کنیم.

1. بیایید ارزش پیمانه اندازه متوسط یک کندل استیک یک دقیقه ای را پیدا کنیم. این مقدار اندازه مرحله خواهد بود. برای این کار قیمت پایانی کندل استیک قبلی را از قیمت پایانی کندل استیک بعدی کم می کنیم و مقدار پیمانه را به دست می آوریم. من اندازه متوسط کندل استیک یک دقیقه ای GBPUSD را برابر 000170 به دست آوردم.
2. حال بیایید اندازه متوسط کندل استیک یک ساعته را برای همان دوره (کندل استیک یک ساعته دارای 60 کندل استیک یک دقیقه ای است) پیدا کنیم. برای این کار قیمت پایانی کندل استیک یک ساعته قبلی را از قیمت پایانی کندل استیک یک ساعته بعدی کم می کنیم و مقدار پیمانه را به دست می آوریم. من اندازه متوسط کندل استیک یک ساعته GBPUSD را برابر 001117 به دست آوردم.
3. اکنون بیایید پیدا کنیم که قیمت چقدر باید به طور متوسط در ساعت عبور کند، اگر در نظر بگیریم که سری های گام تصادفی است. برای این کار، اندازه متوسط کندل استیک یک دقیقه ای را در ریشه دوم تعداد مراحل ضرب و سپس در اندازه متوسط مرحله ضرب می نماییم. 60 مرحله داریم در نتیحه 000170*(60^0.5)=0.001315. اندازه کندل استیک یک ساعته متمایل به این اندازه متوسط است اگر از قانون توزیع نرمال تبعیت کند.
4. حال اندازه کندل استیک واقعی (001117) و کندل استیک گام تصادفی (0.001315) را با هم مقایسه می کنیم. اختلاف فقط به اندازه 0.0002 می باشد. قایل نتیجه گیری است که فرض ما مبنی بر تبعیت اندازه کندل استیک از قانون توزیع نرمال به وسیله داده های بازار نماد واقعی تایید می شود. تفاوت 0.0002 ناچیز است.

بعدا با استفاده از کندل استیک یک ساعته به دست آمده، عملا یک ردیف از چندین بخش سری های قیمت، دامنه های آنهایی که از قانون توزیع نرمال تبعیت می کنند، را ترکیب و تحلیل می کنیم. طبیعتا، اگر به سمت بازه های زمانی بلندتر حرکت کنیم، تمام کندل استیک های مشابه، اندازه آنها متناسب با ریشه دوم تعداد مراحل است، را به دست می آوریم. اکنون به شکل 2 رجوع می کنیم: اگر یک سری به اشتباه گسسته سازی شود، یک ردیف تصادفی به عنوان نتیجه خروجی خواهد بود. در واقع، با استفاده از گسسته سازی زمان، سری های قیمت را به یک ردیف تصادفی تبدیل      نموده ایم. بسیار خب، یک ردیف گسسته سازی شده زمانی کماکان می تواند الگو داشته باشد زیرا بازار یک ردیف تصادفی نیست و وابستگی غیر مستقیم به زمان دارد اما تحلیل چنین سری هایی و تعیین الگوها خیلی سخت تر می شود. همین گسسته سازی زمان است که منجر به نویز و عدم ثبات در سری های قیمت می شود- اغلب موردبحث قرار می گیرند اما هیچ کس توضیح نمی دهد که این نویزها از کجا می آیند. حالا، نویزها نه تنها نویزهای گسسته سازی بازار مالی هستند که هنگام گسسته سازی سیگنال ظاهر می شوند، بلکه شامل مولفه تصادفی می باشند که به دلیل پارامترهای گسسته سازی بازار مالی اشتباه سری های قیمت ظاهر می شوند و خود گسسته است.

جهت اطمینان از اینکه نتایج به دست آمده ما با کندل استیک های یک ساعته یک هماهنگی تصادفی نیستند، همین فرآیند را برای کندل استیک های روزانه تکرار می کنیم. 24 ساعت در یک روز وجود دارد. از آنجاییکه جفت های ارزی در طول ساعت معامله می شوند، اجازه دهید فرض کنیم که کندل استیک روزانه برابر با 1440 کندل استیک یک دقیقه ای است. اجازه دهید فاصله مشابه داده های یک دقیقه ای نمونه بگیریم که برای H1 استفاده کردیم. این بار، داده های مرتبط به شکل جدول برای راحتی ارائه می شود.

جدول اول

Average size of M1 candlestick	Average size of H1 candlestick	Theoretical size of H1 candlestick calculated as 0.000117*(60^0.5)	Average real size of D1 candlestick	Theoretical size of D1 candlestick calculated as 0.00017*(1440^0.5)
0.000170	0.001117	0.001315	0.006547	0.006442

همان طور که می توانید ببینید، اندازه متوسط واقعی کندل استیک روزانه خیلی متفاوت از اندازه پیش بینی شده تئوریک در صورت نبود بازار واقعی به جز داده تصادفی، نمی باشد. فایل اکسل داده های تاریخچه و محاسبات در زیر ضمیمه شده است.

برای محاسبه اندازه متوسط کندل استیک ها در بازه های زمانی بزرگتر، از داده های بازه یک دقیقه ای استفاده کردیم. اما چه می شود اگر پایین تر از داده های تیک به دست آوریم- این امر یک نتیجه متفاوت خواهد داشت؟ چه کار میخواهیم انجام دهیم:

• داده های حجم تیک کندل استیک یک دقیقه ای (از نوع واقعی) برای همان دوره مشابه به دست آورده و تعداد متوسط تیک ها در یک کندل استیک یک دقیقه ای- تعداد متوسط 99 تیک در دقیقه است.
• داده های تیک را بارگذاری نموده و اندازه تیک متوسط را به دست آورید، برابر با 000014378 می باشد.
• اندازه تئوریک کندل استیک یک دقیقه ای را به صورت (59.99^0.5)*0.000014378 =0.000111363 محاسبه کنید.
• اندازه تئوریک کندل استیک یک ساعته را به صورت ((59.99*60)^0.5)*0.000014378 =0.00086 محاسبه کنید.

جدول دوم

Average tick size	Average real M1 candlestick size	Theoretical size of M1 candlestick calculated as (59.99^0.5)*0.000014378	Average size of H1 candlestick	Theoretical size of H1 candlestick calculated ((59.99*60)^0.5)*0.000014378
0.000014378	0.00017	0.000111363	0.001117	0.00086

همان طور که می توانید ببینید، اندازه متوسط کندل استیک M1 و H1 خیلی متفاوت از نوع تئوریک آن، که سری های قیمت با گام تصادفی است،   نمی باشد. بنابراین، می توانیم نتیجه بگیریم که به چند دلیل، سری های قیمت همانند گام تصادفی رفتار می کنند که احتمالا می تواند به دلیل گسسته سازی اشتباه فواصل زمانی باشد.

 

چگالی توزیع افزایش سری های قیمت

ارزیابی کمی اجازه می دهد تا تقریبا تخمین زده شود که چگونه اندازه کندل استیک سری های قیمت مرتبط با اندازه کندل استیک گام تصادفی است. جالب تر است که چگالی توزیع افزایش سری های قیمت را ترسیم کنیم که به ما اجازه میده تا به طور بصری تشابهات و تفاوت ها را با چگالی توزیع افزایش های گام تصادفی ارزیابی نماییم.

بخش مهم تحلیل آماده سازی داده ها می باشد. چگالی افزایش ها برای تعدادی از نقاط محاسبه می شود که قیمت می تواند در 60 دقیقه (یک ساعت)، یعنی 60 مرحله، حرکت کند. در اینجا لازم است تا اندازه متوسط کندل استیک یک دقیقه ای و تعداد مراحل (تعداد کندل استیک های یک دقیقه ای در کندل استیک یک ساعته) را بدانیم. قبلا اندازه متوسط کندل استیک را محاسبه نمودیم- برابر با 0.000170 می باشد. تعداد کندل استیک های یک دقیقه ای در کندل استیک یک ساعته 60 می باشد. یعنی اینکه قیمت میتواند 60 مرحله در ساعت، هر مرحله برابر با 0.000170، بسازد. پس موارد شدید وقتی خواهد بود که قیمت به طور پیوسته 60 نقطه بالاتر یا 60 نقطه پایین تر از نقطه شروع حرکت کند. بنابراین، چگالی توزیع در محدوده بین دو عدد برابر با -0.00017*60=-0.0102 و 0.00017*60=0.0102 تخمین زده خواهد شد. به عبارت دیگر، می دانیم که اگر قیمت فقط بالا رود، در مراحل 0.00017، بنابراین به عدد ماکزیموم 0.0102 در 60 مرحله (یک ساعت) خواهد رسید. به علاوه، برای 60 مرحله، قیمت فقط می تواند سطوح گسسته 0، 0.00034، 0.00068، 0.00102، …، 0.0102 را داشته باشد و برای مقادیر منفی نیز به همین ترتیب است. شکل 6 نشان می دهد که چرا قیمت دقیقا این سطوح را خواهد گرفت.

 

شکل 6

 

اگر چند تابع گسسته از نقطه 0 شروع شوند، مرحله اش برابر با 1 بوده و 6 مرحله می سازد، بنابراین نهایتا به طور عمودی می تواند 6، 4، 2 یا 0 بخش جابجا شود و فقط می تواند مقادیر گسسته ای به اندازه دو برابر اندازه مرحله بگیرد. مورد ما هم مشابه است: اگر اندازه متوسط کندل استیک یک دقیقه ای 0.00017 باشد، بنابراین قیمت می تواند سطوح گسسته ای با فواصلی مساوی دو برابر اندازه کندل استیک بگیرد. در واقعیت، کندل استیک ها    می توانند اندازه های مختلفی، نه فقط 0.00017، داشته باشند، به همین دلیل است که قیمت می تواند مقادیر متوسط بگیرد. بنابراین، برای تحلیل شمارش خواهیم کرد که چه تعداد بخش درون فواصل زمانی برابر با دوبرابر اندازه کندل می شوند. به منظور پیدا کردن تفاوت بین توزیع حاصل برای سری های قیمت، آن را با توزیع گام تصادفی مقایسه کنید. خصوصیات گام تصادفی به گونه ای است که احتمال تغییر جهت هر مرحله 50% بوده و هیچ حافظه ای وجود ندارد. شکل 7 احتمال توزیع های چگالی را به رنگ مشکی برای سری های قیمت و به رنگ قرمز برای گام تصادفی نشان می دهد.

 

شکل 7

از شکل 7 می توان دید که چگالی احتمال توزیع سری های قیمت تقریبا با چگالی احتمال توزیع گام تصادفی مطابق است. چگالی احتمال توزیع سری های قیمت در مقایسه با چگالی احتمال توزیع گام تصادفی به مقدار کمی پیک بالاتری دارد، کمی باریک تر است و کمی بیشتر به راست شیفت پیدا کرده است. این امر توصیه می کند که احتمال قیمت بازگشتی در هر مرحله بعد کمی بالاتر از 50% است و کمی تمایل روبه بالا دارد اما این اختلاف ها زیاد نیستند. شاید به نظر برسد که سوددهی از این انحرافات آنقدر مشکل نیست اما این مورد را در مقاله بعد در نظر خواهیم گرفت. در اینجا با یک متغیر تصادفی ایده آل سر و کار داریم که با یک نمونه بزرگ کافی، به سمت نقطه معیار میل خواهد داشت. گراف احتمال چگالی توزیع برای گام تصادفی با استفاده از یک جدول رسم شده است که بخشی از آن در شکل 8 نشان داده شده است.

شکل 8

 

این گراف احتمال چگالی توزیع نتیجه گیری پیشتر ما را تایید می کند که اندازه کندل استیک (در این مورد کندل استیک H1) متمایل به اندازه کندل استیک با سری قیمت گام تصادفی است. همچنین اجازه ارزیابی این واقعیت را به طور بصری و دقیق تر می دهد. تمام داده ها و محاسبات مذکور در این مقاله در فایل اکسل بالا ضمیمه شده است.

 

نواحی تغییرپذیر بالا و پایین

معامله گران فعال ممکن است توجه نمایند که کندل استیک های بازار به طور مرسوم به دو گروه کندل استیک های بزرگ و کوچک (نواحی تغییر پذیر بالا و پایین) تقسیم می شوند، یعنی اینکه نمودار یک گام تصادفی نبوده و الگوهایی وجود دارد. اگر گسسته سازی زمان انحرافات زیادی می داشت، در نتیجه تاثیرش قابل مشاهده نمی بود. با این وجودف این خصوصیت می تواند به وسیله این واقعیت توضیح داده شود که اندازه کندل استیک وابسته به تعداد انجام معاملات صورت گرفته درون کندل استیک می باشد. این امر چگونه قابل بررسی می باشد؟ به سادگی می توانید به نمودار حجم های تیک نگاه کنید- دوره های کندل استیک کوچک همراه با حجم های تیک پایین می باشند و دوره های کندل استیک بزرگ در کنار دوره های حجم تیک بالا قرار می گیرند. اگر فرض کنیم که یک تیک برابر با یک مرحله باشد، در نتیجه قیمت مراحل بیشتری را در دوره های کندل استیک بزرگ طی می کند اما اندازه کندل استیک متناسب با ریشه دوم تعداد مراحل ضربدر اندازه مرحله متوسط باقی می ماند (نمونه در شکل 9). حجم های تیک، در عوض، مستقیما در رابطه با فعالیت معاملات می باشد: هرچه فعالیت معاملات بیشتر باشد، تیک های بیشتری در واحد زمان طی می شوند. بازارهای ارزی تاریخچه ای از حجم های واقعی فراهم می آورند که در آن می توانید ببینید که حجم های تیک به شدت با حجم های واقعی در ارتباطند که همچنین رابطه بین تعداد تیک ها و شدت فعالیت معاملات را بیان می دارد.

شکل 9

این امر همچنین ثابت می کند که گسسته سازی زمان انحرافات شدیدی در سری های قیمت حاصل اعمال می کند و بنابراین تحلیل قیمت را مشکل تر می نماید. این انحراف به ظهور دسته بندی های مجزایی از سیستم های معاملاتی، به نام night scalpers، منجر شده است. نمی گویم که آنها      می توانند سود تولید کنند اما لازم است که این خاص بودن حضور سری های قیمت، هنگام ارائه چنین سیستم های لحاظ شود و تحقیقات مضاعفی را برای جواب سوال بعدی ایجاد نماید: آیا احتمال بازگشت در این نواحی واقعا بیشتر از احتمال ادامه روند است؟ و آیا خصوصیات آماری این نواحی اجازه می دهد تا سودی تولید شود؟ زیرا چنین سیستم هایی بر اساس چنین الگوهایی می باشند.

 

گسسته سازی سری های قیمت جایگزین

یک نتیجه گیری ساده از تحلیل بالا پیشنهاد می دهد که داده های تیک برای پردازش و تحلیل مناسب تر هستند چرا که آنها از خطاهای گسسته سازی در سری های قیمت اجتناب می کنند. اگر مقیاس بزرگتری نیاز داشته باشیم، بلوک های 10 یا 100 تیک به کار خواهند برد. اما مشکل این است که خود تیک ها همچنین یک روش گسسته سازی هستند. این روش به طور گسترده ای استفاده می شود اما همچنان می تواند انحرافاتی را در پردازش ایجاد کند زیرا قیمت تابع تیک های دریافتی نمی باشد. قیمت حداقل تابعی از معاملات انجام شده است در حالیکه یک معامله ممکن است همیشه تیک تولید نکند. تیک ها در یک تبادل ارزی به گونه ای مرتبط با معامله واقعی هستند. اما در بازار فارکس، هر شرکتی می تواند هر تعدادی از تیک ها را فراهم آورد و فهم اینکه کدام صحیح است، مشکل می باشد. بنابراین، حتی اگر به سادگی فرض کنیم که قیمت تابعی از معاملات است، واضح می شود که تیک ها سری های قیمت را منحرف و یک مولفه تصادفی ایجاد می کنند که می تواند به خطا ختم شود.

مسئله گسسته سازی مناسب بخش مهمی از تحلیل داده ها می باشد. به عنوان مثال، شکل 10 دو نمودار قیمت بیت کوین در برابر دلار را نشان   می دهد. نمودار بالایی نمودار کندل استیک هفته ای معمولی و نمودار پایینی بلوک های گسسته N نقطه می باشد. در یک دوره مشابه و تعداد برابری از یلوک ها/کندل استیک ها، اما با روش های گسسته سازی متفاوت، میباشد. می توانید ببینید که نمودارهای دارایی های مشابه، متفاوت از هم هستند. یک سوال طبیعی پیش می آید: کدام یک از دو نمودار صحیح است؟

شکل 10

 

به این نتیجه رسیدم که نمایش صحیح، نموداری است که طبیعت گسسته سازی سری های قیمت را لحاظ کرده باشد. با این وجود، از آنجاییکه طبیعت گسسته سازی ناشناخته باقی می ماند، استفاده از چنین روش گسسته سازی صحیح تر است که بتواند تولید سود/زیان را هم برای من و هم برای دیگر معامله گران بازار بازتاب دهد. بنابراین، بهتر است که داده ها را براساس اینکه چه درآمدهایی تشکیل شده است، تحلیل کرد. یعنی، نباید حرکت قیمت در زمان را در نظر بگیریم اما باید فقط چقدر قیمت حرکت کرده است را لحاظ نمود.

یک جایگزین برای گسسته سازی زمان می تواند گسسته سازی دامنه ثابت باشد که در آن فرض می شود، قیمت تابعی از خودش می باشد. بلوک هایی وجود دارند که پیشتر بحث کردیم. یک بلوک N نقطه ای فرض می شود که بعد از اینکه قیمت N نقطه عمودی را طی کرد، بسته شود. شاید این بهترین رویکرد نباشد اما علاقه مندیم که دقیقا قیمت چه تعداد نقطه را طی کرده است زیرا این امر بر روی سود یا زیان تولیدی ما اثر می گذارد. علاوه بر این، سود هر معامله گر بعد از اینکه قیمت N نقطه عمودی را طی کرد، تغییر می کند. یعنی اینکه مدلی که در آن قیمت تابعی از خودش می باشد، نزدیکترین مدل به معامله واقعی می باشد. شکل 11 گسسته سازی سینوسی در بلوک های اندازه ثابت را نشان می دهد. شکل از بین رفته است، اما خصوصیات اصلی، شامل دوره و دامنه، حفظ می شود.

شکل 11

حتی اگر پارامترهای گسسته سازی اشتباه تنظیم شوند، مقادیر دامنه و دوره کماکان حفظ خواهند شد. شکل 12 نمونه ای را نشان می دهد که وقتی اندازه بلوک خیلی بزرگ باشد چه اتفاقی می افتد. بخش اطلاعاتی درون بلوک از بین می رود و بنابراین دقت کمتر می شود (در فشردن داده ها اجتناب ناپذیر است) اما اطلاعات درباره دامنه و دوره حفظ می شود. اگر اندازه بلوک بزرگتر از دامنه سری های قیمت باشد، بلوک نمایش داده نخواهد شد. بنابراین، برخلاف شکل 2، اگر پارامترهای گسسته سازی اشتباه انتخاب شوند، سیگنال قطعی اصلی به سیگنال تصادفی تبدیل نخواهد شد.

شکل 12

 

این امر اجازه می دهد تا مولفه تصادفی ایجاد شده توسط سری های قیمت گسسته شده زمانی و در مواقعی که عملکرد پارامتر آن در سری های مرجع معلوم نیست، حذف شود. این روش بهتر از گسسته زمانی زمان نتیجه می دهد و اجازه یک مقیاس بندی راحت نمودار، با دقت تغییرات مقیاس بندی در حدود 1 نقطه، را می دهد.

 

نتیجه گیری

• طبیعت سری های قیمت گسسته است که از ساختار قیمت گذاری نشات می گیرد.
• قیمت بازار تابعی از زمان نیست اما تابعی از فرآیندهای اقتصادی خیلی مرتبط است و در حال حاضر امکان ندارد که تمام آنها لحاظ شوند.
• گسسته سازی بازار مالی سری های قیمت در فواصل زمانی یک مولفه تصادفی مشهود ایجاد می کند؛ این امر شکل واقعی نمودار قیمت را منحرف می کند، نویز و ناپایداری را به این فرآیند پیچیده با پارامترهای ناشناخته اضافه می کند.
• لازم است که پارامتر تاثیرگذار بر روی قیمت لحاظ شود وقتی که روش های گسسته سازی بازار مالی سری های قیمت ارائه می شوند.
• ناپایداری سری های قیمت به دلیل پارامترهای گسسته سازی بازار مالی اشتباه، از میان سایر دلایل، ایجاد می شود.
• نمودارهای قیمت گسسته شده زمانی می توانند به عنوان تلاشی برای یافتن یک الگو تحلیل شوند اما لازم است که جنبه های بالا لحاظ شود تا فهم بهتری از طبیعت الگوی یافته شده و مخصوص داشت.
• هدف ارائه سایر روش های گسسته سازی بازار مالی سری های قیمتی می باشد که انحراف کمتری نسبت به داده های اصلی داشته باشند. یکی از این روش ها در این مقاله توضیح داده شد.
• الگوریتم های معامله و مطالعات آماری بازار می بایست برای در نظر گرفتن خصوصیات ویژه به کار رفته در گسسته سازی بازار مالی سری های قیمت ارائه شوند.

 

این مقاله ترجمه شده توسط تیم آکادمی ایران ام کیو ال می باشد. 

صفحه اصلی مقاله