زبان ام کیو ال یکی از بهترین روش های حل مسائل و معاملات فارکس می باشد. آکادمی ایران ام کیو ال در اینن مقاله قصد دارد شما را با چندین روش حل معامله در زبان ام کیو ال آشنا کند . پیشنهاد می کنیم حتما در دوره آموزش MQL  شرکت کنید. در این دوره به صورت صفر تا صد تمامی نکات  و اصول زبان ام کیو ال یاد داده شده است.

من توسعه دهنده استراتژی ­ها و نرم افزارهای خودکار با بیش از 5 سال تجربه هستم. در این مقاله من، مسائل را برای کسانی که تازه شروع به معامله در فارکس یا هر صرافی دیگر می­کنند، شفاف ­سازی می­کنم. علاوه بر این، من سعی می­کنم به متداول­ترین سوالات معامله ­ای پاسخ دهم.

امیدوارم این مقاله برای معامله ­گران مبتدی و باتجربه مفید باشد. هم­چنین، توجه داشته باشید که این صرفاً چشم­انداز من بر اساس تجربه و تحقیقات واقعی است.

برخی از ربات­ ها و شاخص­ه ای ذکر شده را می­توان در محصولات من یافت. اما این فقط یک قسمت کوچک است. من طیف گسترده­ای از ربات­ ها را توسعه داده­ ام که تعداد زیادی استراتژی را به کار می­گیرند. من سعی خواهم کرد نشان دهم که چگونه روش توصیف شده می­تواند بینشی در مورد ماهیت واقعی بازار داشته باشد و کدام یک از استراتژی­ ها قابل توجه است.

چرا یافتن نقاط ورود و خروج، چالش برانگیز است ( زبان ام کیو ال ) ؟

اگر ورود به بازار و خروج از بازار را می­دانید، احتمالاً نیازی به دانستن چیز دیگری ندارید. متاسفانه، مسئله ورود/ خروج موضوعی است که به سختی قابل دستیابی است. در نگاه اول، همیشه می­توانید الگویی را شناسایی کرده و مدتی آن را دنبال کنید. اما چگونه می­توان آن را بدون ابزارها و شاخص­ه ای پیچیده تشخیص داد؟ ساده ­ترین و تکراری­ترین الگوها TREND و FLAT هستند. TREND یک حرکت طولانی مدت در یک جهت است، در حالی که Flat به طور مکرر معکوس می­شود.

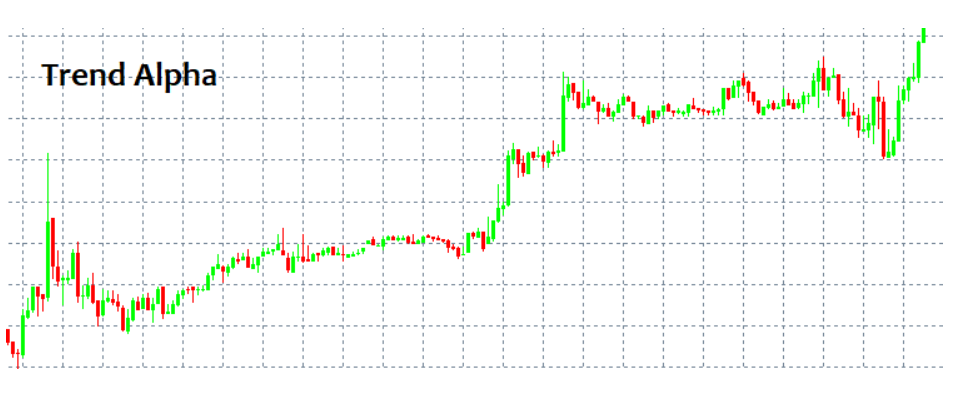
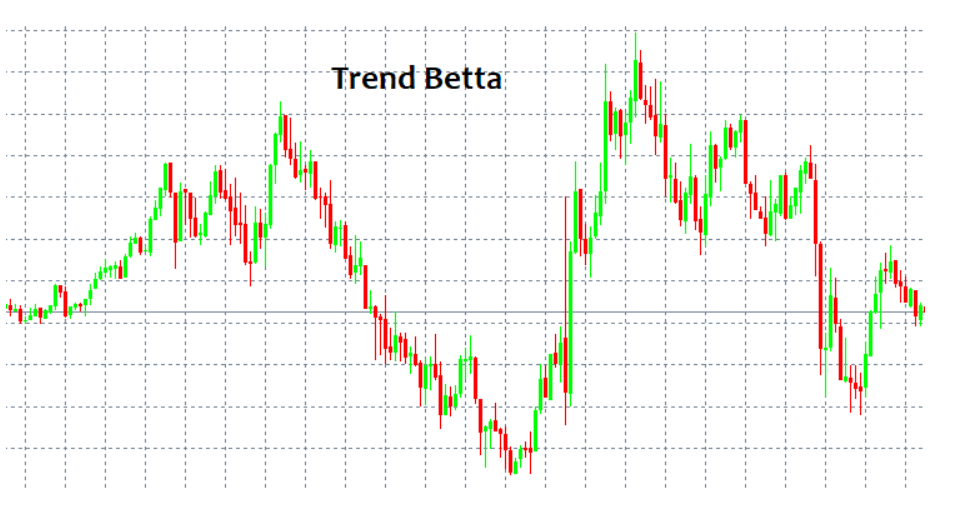
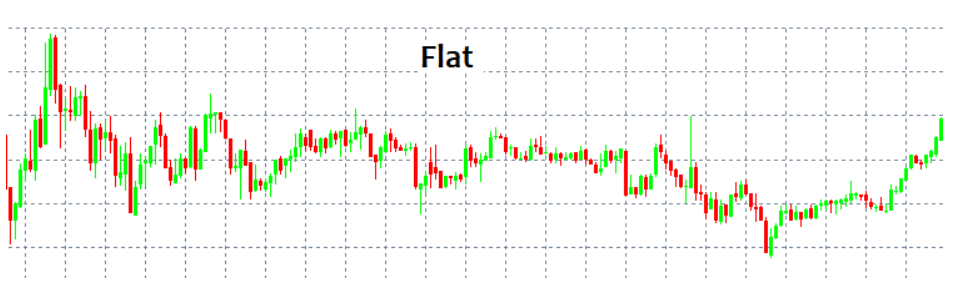
این الگوها به راحتی قابل تشخیص هستند زیرا چشم انسان می­تواند آن­ ها را بدون هیچ شاخصی پیدا کند. مسئله اصلی در این­جا این است که ما فقط پس از ایجاد یک الگو می­توانیم آن را ببینیم. علاوه بر این، هیچ کس نمی­تواند تضمین کند که اصلاً الگویی وجود ندارد. بدون در نظر گرفتن استراتژی، هیچ الگویی نمی­تواند سپرده شما را از نابودی نجات دهد. سعی خواهم کرد با استفاده از زبان ریاضی دلایل احتمالی این موضوع را ارائه دهم.

سازوکارها و سطوح بازار در زبان ام کیو ال

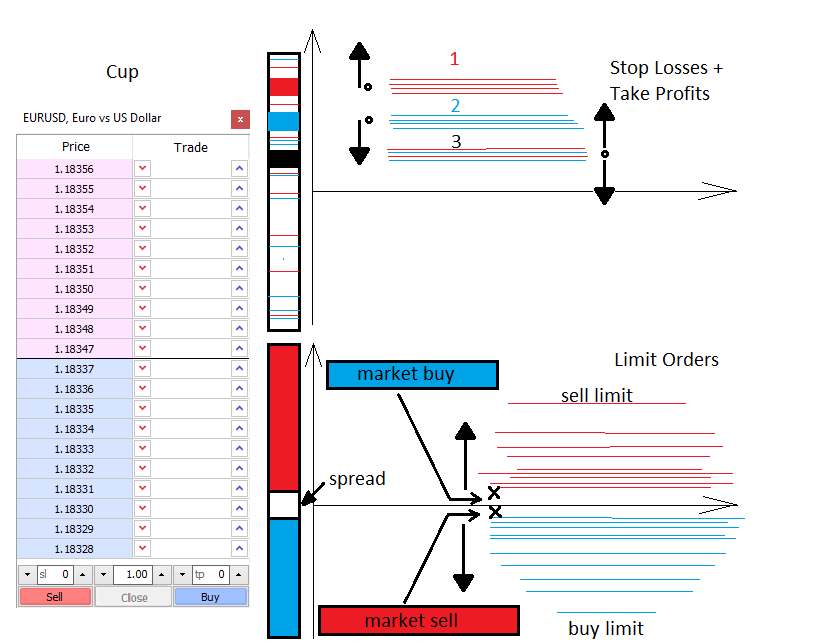
بگذارید کمی در مورد قیمت­ گذاری و قدرت­ هایی که باعث حرکت قیمت بازار می­شوند برای شما صحبت کنم. دو نیرو در بازار وجود دارد – نیروی بازار و نیروی محدود. به همین ترتیب، دو نوع سفارش وجود دارد – سفارش­ های بازار و سفارش­ های محدود. خریداران و فروشندگان محدود، عمق بازار را پر می­کنند، در حالی که بازار آن را از هم جدا می­کند. عمق بازار اساساً مقیاس عمودی قیمت است که نشان دهنده کسانی است که مایل به خرید یا فروش چیزی هستند. همیشه بین فروشندگان و خریداران محدود، گپ وجود دارد. به این گپ، spread گفته می­شود. Spread فاصله ­ای است بین بهترین قیمت ­های خرید و فروش که در تعداد حداقل تغییرات قیمت اندازه ­گیری شده است. خریداران می­خواهند با ارزان ­ترین قیمت خرید کنند در حالی که فروشندگان می­خواهند با بالاترین قیمت بفروشند. بنابراین، سفارشات محدود خریداران همیشه در پایین قرار دارند، در حالی که سفارشات فروشندگان همیشه در بالا قرار دارند. خریداران و فروشندگان Marker وارد عمق بازار می­شوند و دو سفارشی (سفارشات محدود و بازار) به هم پیوند می­خورند. حرکت بازار زمانی اتفاق می­افتد که یک سفارش محدود اعمال شود.

وقتی یک سفارش فعال در بازار پدیدار می­شود، معمولاً Stop Loss و Take Profit دارد. مشابه سطح سفارشات محدود، این stop level در سطح بازار پراکنده شده و شتاب قیمت یا سطح معکوس را تشکیل می­دهد. همه چیز به میزان و نوع stop level و هم­چنین میزان معامله بستگی دارد. با دانستن این سطوح، می­توان گفت که در کجا ممکن است قیمت تسریع یابد یا معکوس شود.

سفارشات محدود نیز می­تواند نوسانات و خوشه­ هایی ایجاد کند که عبور از آن­ ها دشوار است. آن­ ها معمولاً در نقاط مهم قیمت مانند باز شدن یک روز یا یک هفته ظاهر می­شوند. هنگام بحث در مورد معاملات مبتنی بر سطح، معامله گران معمولاً استفاده از سطح سفارشات محدود را دارند. همه این­ها را می­توان به صورت خلاصه به شرح زیر نمایش داد

شرح ریاضی بازار

آن­چه در پنجره MetaTrader می­بینیم یک تابع گسسته از آرگومان t است، که در این­جا t زمان است. این تابع گسسته است زیرا تعداد tickها محدود است. در حالت فعلی، tickها نقاطی هستند که حاوی هیچ چیزی در این بین نیستند.

tickها کوچک­ترین عناصر ممکن برای گسسته ­سازی قیمت هستند، عناصر بزرگ­تر میله­ ها هستند، کندل­ ها M1 ، M5 ، M15 و غیره هستند. بازار از هر دو عنصر تصادفی و الگو برخوردار است. الگوها می­توانند مقیاس و مدت زمان مختلفی داشته باشند. با این حال، بازار در بیش­تر موارد یک محیط احتمالی، chaotic و تقریباً غیر قابل پیش­بینی است. برای درک بازار، باید آن را از طریق مفاهیم نظریه احتمال مشاهده کرد. گسسته ­سازی برای معرفی مفاهیم احتمال و چگالی احتمال مورد نیاز است.

برای معرفی مفهوم بازده مورد انتظار، ابتدا باید اصطلاحات “رویداد” و “رویدادهای جامع” را در نظر بگیریم:

• رویداد C1 – سود، برابر است با tp
• رویداد C2 – ضرر، برابر است با sl
• P1 – احتمال وقوع C1
• P2 – احتمال وقوع C2

رویدادهای С1 و С2 گروه کاملی از رویدادهای متضاد را تشکیل می­دهند (یعنی در هر صورت یکی از این رویدادها رخ می­دهد). بنابراین، مجموع این احتمالات برابر است با یک 1= P2(tp,sl) +P2(tp,sl) است. این معادله بعداً ممکن است مفید باشد. هنگام تست اکسپرت ادوایزر یا یک استراتژی دستی با شروع تصادفی، و هم­چنین

StopLoss و TakeProfit تصادفی، باز هم یک نتیجه غیر تصادفی و بازده مورد انتظاری برابر با “- (Spread)” به دست می­آوریم، که به معنای “0” است، اگر ما می­توانیم Spread را به صفر برسانیم. این نشان می­دهد که ما همیشه در بازار تصادفی بدون در نظر گرفتن stop level، بازده صفر پیش­بینی شده داریم. در بازار غیر تصادفی، به شرط آن­که بازار از الگوی مربوطه برخوردار باشد، همیشه سود یا زیان به دست می ­آوریم.

با فرض این­که بازده مورد انتظار (-Tick[0].Bid  Tick[1].Bid) نیز برابر با صفر است، می­توانیم به همان نتایج برسیم. این­ها نتایج کاملاً ساده­ای است که از بسیاری جهات می­توان به آن­ها رسید.

• M=P1*tp-P2*sl=P1*tp-(1-P1)*sl- برای هر بازاری
• P1*tp-P2*sl- برای بازار chaotic

حل معاملات chaotic در زبان ام کیو ال

این معادله اصلی بازار chaotic است که توصیف بازده مورد انتظار و باز و بسته شدن سفارش chaotic را با استفاده از stop level توصیف می­کند. پس از حل آخرین معادله، تمام احتمالاتی را که به آن علاقه­مند هستیم، هم برای تصادفی کامل و هم برای حالت مقابل، به شرط آن­که مقادیر stop  را بدانیم، به دست می­آوریم.

معادله ارائه شده در این­جا تنها برای ساده­ترین حالت قابل تعمیم برای هر استراتژی است. این دقیقاً همان کاری است که من اکنون می­خواهم انجام دهم تا به درک کاملی از آن­چه که آخرین بازده مورد انتظار که ما باید آن را غیر صفر کنیم، دست یابم. هم­چنین، بیایید مفهوم ضریب سود را معرفی کنیم و معادلات مناسب را بنویسیم.

فرض کنید که استراتژی ما شامل بسته شدن، هم با stop level و هم با برخی از سیگنال­های دیگر است. برای این کار، من فضای رویداد С3، С4 را معرفی می­کنم که در آن رویداد اول با stop level بسته می­شود، در حالی که رویداد دوم با سیگنال بسته می­شود. آن­ها هم­چنین یک گروه کاملی از رویدادهای متضاد را تشکیل می­دهند، بنابراین ما می­توانیم از قیاس منطقی برای نوشتن استفاده کنیم:

M=P3*M3+P4*M4=P3*M3+(1-P3)*M4

در اینجا                                  M3=P1*tp-(1-P1)*sl

در حالی که           M4= Sum (P0[i]*pr[i])-Sum(P01[j]*ls[j]);Sum(P0[i])+Sum(P01[j])=1

• M3 – بازده مورد انتظار هنگام بسته شدن با stop order
• M4- بازده مورد انتظار هنگام بسته شدن با سیگنال
• P1 ، P2- احتمال فعال شدن stop level به شرطی که در هر صورت یکی از stop level ها فعال شود
• P0[i]- احتمال بستن معامله با سود pr[i] به شرطی که باعث stop level نشده باشد. i – شماره گزینه بسته شدن
• P01[j]- احتمال بستن معامله با ضرر ls [j] به شرطی که باعث stop level نشده باشد. j – شماره گزینه بسته شدن

به عبارت دیگر، ما دو رویداد متضاد داریم. نتایج آن­ها دو فضای رویداد مستقل دیگری را تشکیل می­دهد که در آن ما گروه کاملی را نیز تعریف می­کنیم. با این حال، احتمال P1 ، P2 ، P0 [i] و P01 [j] اکنون شرطی هستند، در حالی که P3 و P4 احتمالات فرضیه ­ها هستند. احتمال شرطی، احتمال وقوع یک رویداد در هنگام وقوع یک فرضیه است. همه چیز دقیقاً مطابق با فرمول احتمال کل (فرمول بیز) است. من اکیداً توصیه می­کنم مطالعه کامل آن را انجام دهید تا موضوع را درک کنید. برای یک معامله کاملاً chaotic، M = 0 است.

حتما ثبت نام کنید : آموزش MQL در آکادمی ایران ام کیو ال

اکنون معادله، واضح ­تر و گسترده ­تر شده است، زیرا بسته شدن، هم با stop level و هم با سیگنال را در نظر می­گیرد. ما می­توانیم این قیاس منطقی را حتی بیش­تر دنبال کنیم و معادله عمومی را برای هر استراتژی که حتی stop level های پویا را در نظر می­گیرد، بنویسیم. این همان کاری است که من قصد دارم انجام دهم. بیایید N رویداد جدید را تشکیل دهیم که یک گروه کامل به معنای افتتاح معاملات با StopLoss و TakeProfit مشابه است. CS [1] .. CS [2] .. CS [3] ……. CS [N]. به همین ترتیب

PS [1] + PS [2] + PS [3] + ……. + PS [N] = 1.

M=PS[1]*MS[1]+PS[2]*MS[2]+…+ PS[k]*MS[k] …+PS[N]*MS[N],

MS[k]= P3[k]*M3[k]+(1- P3[k])*M4[k],  M3[k] =  P1[k] *tp[k] -(1- P1[k] )*sl[k],

M4[k]=  Sum(i)(P0[i][k]*pr[i][k])- Sum(j)(P01[j][k] *ls[j][k] );

Sum(i)( P0[i][k]  )+  Sum(j)( P01[j][k]  ) =1.

• PS[k]- احتمال تنظیم گزینه kامین stop level.
• MS[k]- بازده مورد انتظار معاملات بسته با kامین stop level.
• M3[k]- بازده مورد انتظار هنگام بسته شدن با یک stop order با kامین stop level.
• M4[k]- بازده مورد انتظار هنگام بسته شدن توسط سیگنال با kامین stop level.
• P1[k] ، P1[k] – احتمال فعال شدن stop level به شرطی که در هر صورت یکی از stop level ها فعال شود.
• P0[i][k]- احتمال بسته شدن معامله با سود pr[i][k] با توجه به سیگنالی با kامین stop level. i – شماره گزینه بسته شدن
• P01[j][k] – احتمال بسته شدن معامله با ضرر ls[j][k]، با توجه به سیگنالی با stop level. j – شماره گزینه بسته شدن

مانند معادلات قبلی (ساده ­تر)، در مورد معامله chaotic  و عدم وجود spread، M = 0 است. بیش­ترین کاری که می­توانید انجام دهید تغییر استراتژی است اما اگر هیچ پایه منطقی نداشته باشد، شما به سادگی تعادل این متغیرها را تغییر می­دهید و هم­چنان 0 را به دست می آورید. برای از بین بردن این تعادل ناخواسته، باید از احتمال حرکت بازار در هر جهتی با هر بخش حرکت ثابت در نقاط یا بازده مورد انتظار حرکت قیمت در یک بازه زمانی مشخص اطلاع داشته باشیم . نقاط ورود / خروج، بسته به آن انتخاب می­شوند. اگر موفق به یافتن آن­ها شوید، یک استراتژی سود آور خواهید داشت.

حال بیایید معادله ضریب سود را ایجاد کنیم.  =PFسود / ضرر. عامل سود نسبت سود به ضرر است. اگر تعداد از 1 بیش­تر شود، استراتژی سودآور است، در غیر این صورت، این­گونه نیست. با استفاده از بازده مورد انتظار می­توان این مورد را دوباره تعریف کرد PrF=Mp/Mlاین به معنی نسبت بازده سود خالص پیش بینی شده به ضرر خالص مورد انتظار است. بیایید معادلات آن­ها را بنویسیم.

• Mp = PS[1]*MSp[1]+PS[2]*MSp[2]+ … + PS[k]*MSp[k] … +PS[N]*MSp[N] , MSp[k] = P3[k]*M3p[k]+(1- P3[k])*M4p[k] ,  M3p[k] =  P1[k] *tp[k], M4p[k] =  Sum(i)(P0[i][k]*pr[i][k])
• Ml = PS[1]*MSl[1]+PS[2]*MSl[2]+ … + PS[k]*MSl[k] … +PS[N]*MSl[N] , MSl[k] = P3[k]*M3l[k]+(1- P3[k])*M4l[k] ,  M3l[k] =   (1- P1[k] )*sl[k], M4l[k] =  Sum(j)(P01[j][k]*ls[j][k])

Sum(i)( P0[i][k] )+  Sum(j)( P01[j][k]  ) =1.

• MSp[k]: بازده مورد انتظار معاملات بسته شده با kامین stop level.
• MSl[k]: بازده مورد انتظار معاملات بسته شده با kامین stop level.
• M3p[k]: بازده مورد انتظار هنگام بسته شدن با یک stop order با kامین stop level.
• M4p[k]: بازده مورد انتظار هنگام بسته شدن توسط سیگنال با kامین stop level.
• M3l[k]  : ضرر پیش بینی شده هنگام بسته شدن با stop order با kامین stop level.
• M4l[k]: ضرر مورد انتظار هنگام بسته شدن توسط سیگنال با kامین stop level.

برای درک عمیق­تر، من همه وقایع تو در تو را به تصویر می­کشم:

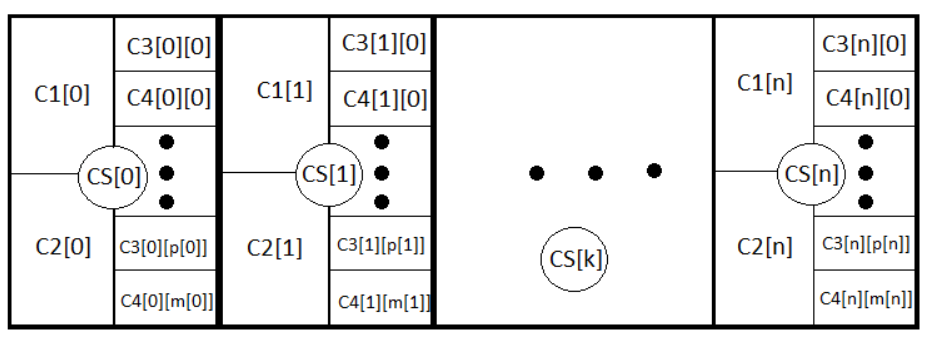
در حقیقت، این همان معادلات هستند، اگرچه معادله اول فاقد قسمت مربوط به ضرر است، در حالی که مورد دوم فاقد قسمت مربوط به سود است. در مورد معاملات chaotic، PrF = 1، spreadای را ارائه می­دهد  که بازهم برابر صفر باشد. M و PrF دو مقداری هستند که برای ارزیابی استراتژی از هر طرف کاملاً کافی هستند.

به طور خاص، توانایی ارزیابی ماهیت trend یا flat یک ابزار خاص با استفاده از همان تئوری احتمال و ترکیبات است. علاوه بر این، هم­چنین می­توان با استفاده از چگالی توزیع احتمال تفاوت­هایی را از تصادفی بودن پیدا کرد.
یک نمودار چگالی توزیع احتمال، مقدار تصادفی برای یک قیمت گسسته در یک مرحله ثابت H در نقاط ایجاد می­کنیم. بیایید فرض کنیم اگر قیمت H به هر جهتی حرکت کند، یک قدم برداشته شده است. محور X برای نشان دادن یک مقدار تصادفی به شکل یک حرکت عمودی نمودار قیمت است که در تعداد مراحل، اندازه گیری شده است. در این حالت، n مرحله ضروری است زیرا این تنها راه ارزیابی حرکت کلی قیمت است.

• n- تعداد کل مراحل (مقدار ثابت)
• d- تعداد مراحل کاهش قیمت
• u- تعداد مراحل افزایش قیمت
• s- حرکت به سمت بالا به صورت مرحله­ای

پس از تعریف این مقادیر، u و d را محاسبه کنید:

برای تهیه مراحل کلی “s” رو به بالا (مقدار می­تواند منفی باشد به معنای مراحل رو به پایین)، باید تعداد مشخصی از مراحل بالا و پایین ارائه شود: “” u ، “d”. حرکت ” s ” نهایی بالا یا پایین در مجموع به همه مراحل بستگی دارد:

n=u+d;

s=u-d;

این یک سیستم دو معادله ­ای است. حل آن باعث به دست آمدن u  و d می­شود:

u=(s+n)/2, d=n-u.

با این حال، همه مقادیر “s” برای یک مقدار خاص “n” مناسب نیستند. گام بین مقادیر s ممکن است همیشه برابر با 2 باشد. این کار به منظور تامین مقادیر طبیعی “u” و “d” انجام می­شود زیرا آن­ها برای ترکیب کننده­ها یا بهتر بگوییم برای محاسبه ترکیبات استفاده می­شوند. اگر این اعداد کسری باشند، بنابراین نمی­توان فاکتوریل را محاسبه کرد که سنگ بنای تمام ترکیبات است. در زیر همه سناریو های ممکن برای 18 مرحله آورده شده است. نمودار نشان می­دهد که گزینه­ های رویداد چه قدر گسترده هستند.

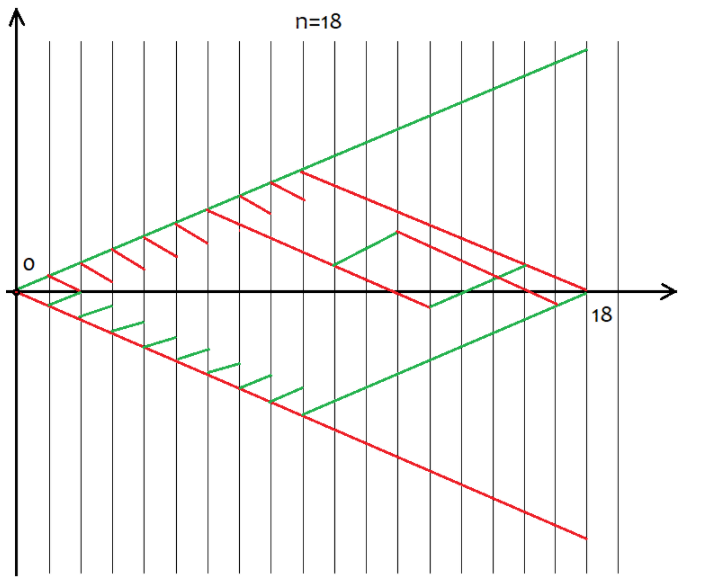
به راحتی می­توان تعریف کرد که تعداد n ^ 2 گزینه را برای کل گزینه­ های قیمت گذاری تشکیل می­دهد، زیرا بعد از هر مرحله فقط دو جهت حرکت وجود دارد – بالا یا پایین. نیازی به تلاش برای درک هر یک از این گزینه­ ها نیست، زیرا این کار غیرممکن است. درعوض ما فقط کافی است بدانیم که n سلول منحصر به فرد داریم که u و d از آن­ها به ترتیب باید بالا و پایین باشند. گزینه­های دارای u و d یکسان در نهایت همان s را فراهم می­کنند.

برای محاسبه تعداد کل گزینه­های ارائه دهنده “s” مشابه، می­توانیم از معادله ترکیبی از ترکیبات С = n! / (u! * (nu)!) و هم­چنین معادله معادل С=n!/(d!*(n-d)!) استفاده کنیم. در مورد u و d متفاوت، مقدار یکسان C را به دست می­آوریم. از آن­جا که ترکیبات را می­توان هم با بخش­ های صعودی و هم نزولی ایجاد کرد، این امر به déjà vu می­انجامد. بنابراین چه بخش­هایی را باید برای تشکیل ترکیبات استفاده کنیم؟ پاسخ، هر چیزی است، زیرا این ترکیبات علی رغم تفاوت­ هایشان برابر هستند. سعی می­کنم با استفاده از یک نرم­افزار مبتنی بر MathCad 15 این موضوع را در زیر ثابت کنم.

حتما ثبت نام کنید : دوره پیشرفته MQL4

اکنون که تعداد ترکیبات مربوط به هر سناریو را تعیین کرده­ایم، می­توانیم احتمال یک ترکیب خاص (یا هر رویدادی را که دوست دارید) تعیین کنیم. P = С / (2 ^ n). این مقدار را می­توان برای همه “s” محاسبه کرد، و مجموع این احتمالات همیشه برابر با 1 است، زیرا به هر حال یکی از این گزینه­ها اتفاق خواهد افتاد. بر اساس این آرایه احتمال، با توجه به این­که گام s ، 2 است، می­توان نمودار چگالی احتمال را نسبت به مقدار تصادفی “s” ایجاد کرد. در این حالت، چگالی یک گام خاص را می­توان به سادگی با تقسیم احتمال بر اندازه گام s، یعنی بر  2 به دست آورد.

دلیل این امر این است که ما قادر به ایجاد یک تابع پیوسته برای مقادیر گسسته نیستیم. این چگالی به نیم قدم به چپ و راست یعنی 1 بستگی دارد. این به ما کمک می­کند نود­ها را پیدا کنیم و امکان ادغام عددی را فراهم می­کند. برای مقادیر “s”  منفی، من نمودار را به نسبت محور چگالی احتمال منعکس می­کنم. برای مقادیر زوج n، شماره­ گذاری نودها از 0 شروع می­شود، برای موارد فرد از 1 شروع می­شود. در مورد مقادیر زوج n، ما نمی­توانیم مقادیر فرد را ارائه دهیم، در حالی که در مورد مقادیر فرد، نمی­توان مقادیر زوج s را ارائه داد. تصویر برنامه محاسبه زیر این را روشن می­کند:

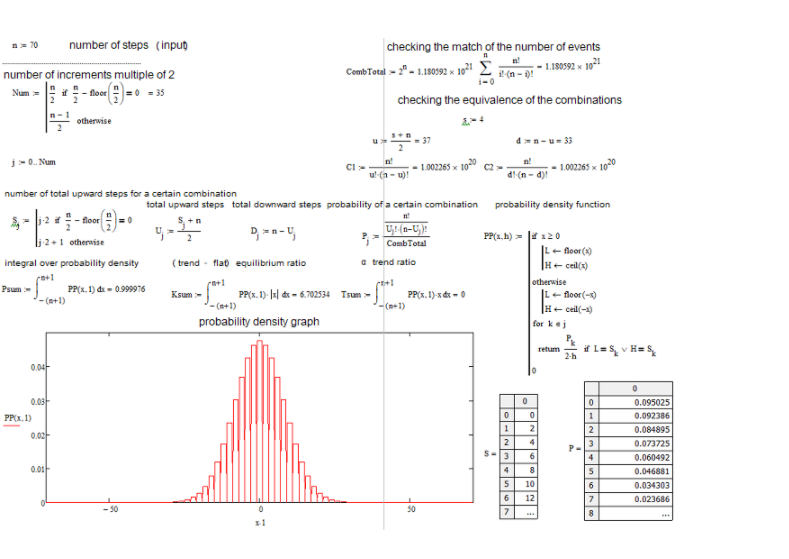
این لیست هر آن­ چیزی است که ما نیاز داریم. برنامه در زیر پیوست شده است تا بتوانید با پارامترها بازی کنید. یکی از محبوب­ ترین سوال ­ها این است که چگونه می­توان تعریف کرد که آیا وضعیت فعلی بازار مبتنی بر trend است یا flat. من معادلات خودم را برای تعیین کمیت trend یا ماهیت flat یک ابزار آورده­ام. من trendها را به آلفا و بتا تقسیم کرده­ام. آلفا به معنای تمایل به خرید یا فروش است، در حالی که بتا فقط تمایل به ادامه حرکت بدون نفوذ مشخصی از خریداران یا فروشندگان است. در نهایت، flat به معنای تمایل به بازگشت به قیمت اولیه است.

تعاریف trend و flat در بین معامله­ گران بسیار متفاوت است. من در تلاش هستم تا تعریف سخت­ تری از همه این پدیده ها ارائه دهم، زیرا حتی درک اساسی از این موارد و ابزارهای کمی ­سازی آن­ها امکان استفاده از بسیاری از استراتژی­هایی را که قبلاً از بین رفته یا بیش از حد ساده تلقی می­شدند، فراهم می­کند. در این­جا این معادلات اصلی وجود دارد:

K=Integral(p*|x|)

یا

K=Summ(P[i]*|s[i]|)

گزینه اول برای یک متغیر تصادفی پیوسته است، در حالی که گزینه دوم برای یک متغیر گسسته است. من مقدار گسسته را برای وضوح بیش­تر پیوسته ساخته­ام، بنابراین از معادله اول استفاده می­کنم. انتگرال از منفی تا مثبت بی نهایت اضافه می­شود. این نسبت موازنه یا نرخ trend است. پس از محاسبه آن برای یک مقدار تصادفی، یک نقطه تعادل به دست می­آوریم که برای مقایسه توزیع واقعی ذکر قیمت سهام با یک مرجع استفاده می­شود. اگر Кp> K، بازار را می­توان trend ارزیابی کرد. اگر Кp <K، بازار، flat است.

بیشتر بدانید : 3 ویژگی منحصر به فرد MQL5 | آشنایی بیشتر با ویژگی­ های زبان MQL5

ما می­توانیم حداکثر مقدار نسبت را محاسبه کنیم. آن برابر است با KMax = 1 * Max (| x |) یا KMax = 1 * Max (| s [i] |). هم­چنین می­توانیم حداقل مقدار نسبت را محاسبه کنیم. آن برابر است با KMin = 1 * Min (| x |) = 0 یا KMin = 1 * Min (| s [i] |) = 0. نقطه میانی KMid، حداقل و حداکثر تمام مواردی است که برای ارزیابی ماهیت حوزه مورد تجزیه و تحلیل درصدی trend یا flat لازم است.

if ( K >= KMid ) KTrendPercent=((K-KMid)/(KMax-KMid))*100  else  KFletPercent=((KMid-K)/KMid)*100.

اما این هنوز برای توصیف کامل شرایط کافی نیست. این­جا جایی است که نسبت دوم T=Integral(p*x)، T = Summ (P [i] * s [i]) به کمک شما می­آید. در اصل بازده مورد انتظار برای تعداد مراحل صعودی را نشان می­دهد و در عین حال شاخص alpha trend است. Tp> 0 به معنای buy trend است، در حالی که Tp <0 به معنای sell trend است، یعنی T = 0 برای مسیر تصادفی است.

بیایید حداکثر و حداقل مقدار نسبت را پیدا کنیم: TMax = 1 * Max (x) یا TMax = 1 * Max (s [i])، مینیمم یکی در مقدار مطلق برابر با ماکزیمم دیگری است، اما به سادگی منفی است TMin = – TMax. اگر درصد alpha trend را از 100 به 100- اندازه گیری کنیم، ممکن است معادلاتی را برای محاسبه مقدار مشابه قبلی بنویسیم:

APercent=( T /TMax)*100.

اگر درصد مثبت باشد، trend، صعودی است، اگر منفی باشد، trend، نزولی است. در مواردی ممکن است مختلط باشد. ممکن است alpha flat و alpha trend وجود داشته باشد اما به طور همزمان trend و flat نباشد. در زیر یک تصویر گرافیکی از عبارات بالا و نمونه­ هایی از نمودارهای چگالی ساخته شده برای تعداد مراحل مختلف آورده شده است.

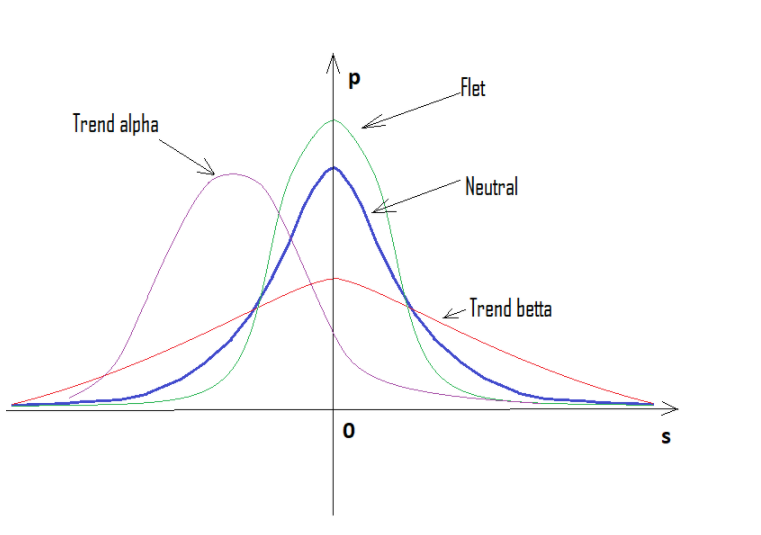
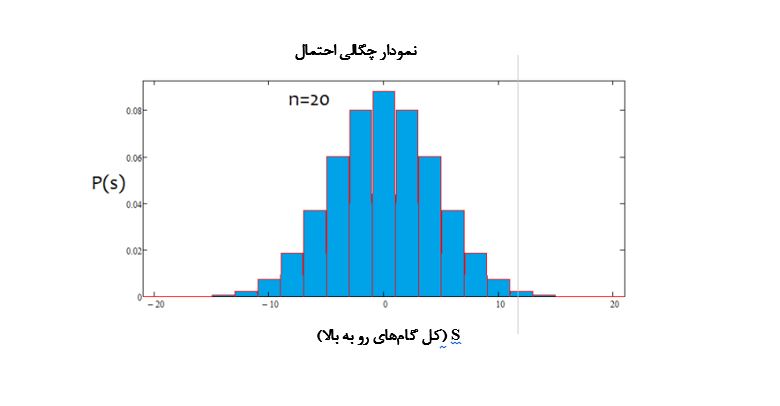
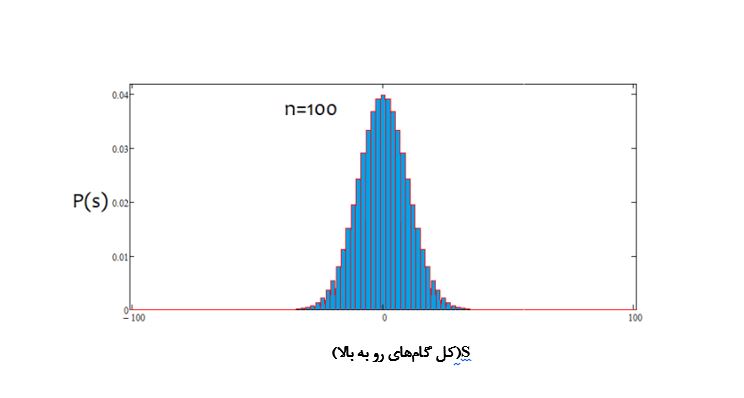
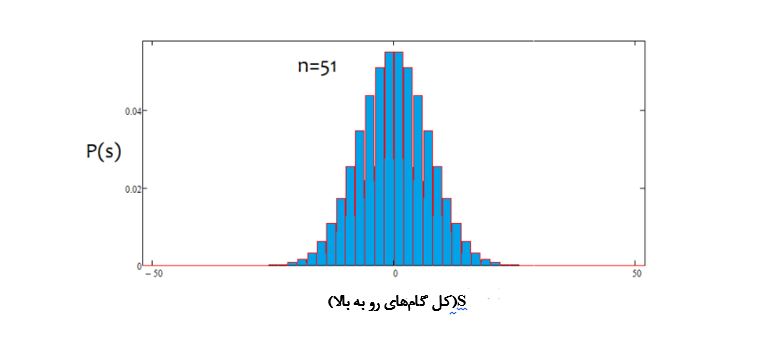
همان­طور که می­بینیم، با افزایش تعداد مراحل، نمودار، باریک­تر و بالاتر می­شود. برای هر تعداد مرحله، مقادیر مربوط به آلفا و بتا متفاوت است، دقیقاً مانند خود توزیع. هنگام تغییر تعداد مراحل، توزیع مرجع باید دوباره محاسبه شود.

تمام این معادلات را می­توان برای ساخت سیستم­های معامله خودکار استفاده کرد. از این الگوریتم­ها می­توان برای توسعه indicator ها نیز استفاده کرد. برخی از معامله­گران قبلاً این موارد را در EAهای خود اجرا کرده­اند. من به یک چیز مطمئن هستم: بهتر است این تجزیه و تحلیل را به جای اجتناب از آن اعمال کنید. کسانی که با ریاضیات آشنا هستند بلافاصله با ایده­های جدیدی در مورد نحوه استفاده از آن آشنا می­شوند. کسانی که نیستند باید بیش­تر تلاش کنند.

این مقاله ترجمه شده توسط تیم آکادمی ایران ام کیو ال می باشد. 

صفحه اصلی مقاله

for_MathCad_15.zip