در این مقاله، من قصد دارم با استفاده از ریاضی و برنامه نویسی در این استراتژی ها تحقیق کرده و سودآوری آنها را ارزیابی کنم. این مقاله دارای بخش های ریاضی و عملی است. در بخش ریاضیات، معادلاتی را برای محاسبه بازده مورد انتظار از استراتژی ها و سایر پارامترهای مهم ارائه میکنم که توسط بسیاری از معامله گران در نظر گرفته نشده است. در بخش عملی، من یک سیستم معاملاتی grid و martingale ساده ایجاد میکنم و معادلات را با واقعیت، مقایسه میکنم. این مقاله به ویژه برای مبتدیان بسیار مفید است زیرا این راهکارها معمولاً اولین راهکارهایی هستند که با آن روبه رو میشوند. اعتقاد کورکورانه به آنها ممکن است منجر به ناامیدی و اتلاف وقت شود، همانطور که در آن زمان برای من اتفاق افتاد. اگر من ریاضیات را نمیدانستم، شاید هنوز هم به آنها اعتقاد داشتم. اما هنوز هم اگر به درستی به این استراتژی ها نگاه کنید منطقی هستند. این همان چیزی است که من میخواهم ثابت کنم.
سیستم معاملاتی این دو استراتژی چه چیزهای مشترکی دارند؟
برای درک محبوبیت این دو استراتژی، باید نگاهی به آنچه همه معامله گران تازه کار فارکس میخواهند، داشته باشیم. بیشتر معامله گران تازه کار، ریاضیدانان و رویاپردازانی هستند که فکر میکنند عقل آنها میتواند به آنها کمک کند تا به سرعت و به راحتی ثروتمند شوند. من هم روزی چنین رویاپردازی بودم. هر دوی این استراتژی ها به شکل نمودارهای سودآوری که به طور مداوم در استراتژی تستر افزایش مییابند، نمایان میشوند. در بسیاری از بخش های اعلام قیمت سهام، تستر ممکن است حتی بدون فیلتر هم نتایج مشابه Grail را نشان دهد. در هر زمینه فعالیتی و در هر کسب و کاری این خطر وجود دارد که افراد آگاهتر بتوانند با هزینه شما خود را غنی کنند. معامله فارکس نیز از این قاعده مستثنی نیست. فارکس، به مقدار زیادی از این قبیل اقدامات فریبنده برخوردار است و این دو استراتژی، بارزترین و مشهورترین اثبات این موضوع است. اولین باری که از این استراتژی ها استفاده میکنید، میبینید که آنها روی همه جفت ارزها با فاکتورهای سود باورنکردنی و بازده مورد انتظار کار میکنند و حتی میتوانند با هرگونه spread کنار بیایند، بنابراین به نظر میرسد که این الگوریتم فراتر از بازار است. دلیل این امر آن است که آنها مبتنی بر ریاضیات محض و بدون منطق هستند. حتی پس از گذشت این همه سال، من همچنان دوست دارم الگوریتم هایی پیدا کنم که به من امکان میدهد بدون توجه به جهت قیمت، همیشه سود کسب کنم. ریاضیدانان به طور کلی افراد جالبی هستند. آنها فارغ از صحت این واقعیت، قادر به اثبات هر چیزی با معادلات صحیح هستند. به طور كلی، این دو استراتژی برای جلب نظر شما در استفاده از آنها، از توهم رسیدن به نقطه سر به سر استفاده میكنند. هر دوی آنها هنوز هم روی هر جفت ارز و هر دورهای کار میکنند، یا بهتر است بگوییم این توهم را در شما ایجاد میکنند تا شما را در مورد سادگی و کارآییشان متقاعد کنند. با کاوش در این استراتژی ها، دیر یا زود متوجه خواهید شد که چیزی نمیدانید. با این حال، این مرحله ضروری است زیرا این تنها راه شروع تفکر منطقی و درک ماهیت واقعی بازار است و اینکه واقعاً از چه راهکارهایی باید استفاده کنید.
سیستم معاملاتی Grid ومعادلات اساسی آن
سیستم معاملاتی Grid سفارشی با هدف سودآوری در هر بازار ایجاد شده است. اگر بازار، دارای حرکتی کاملاً مشهود باشد، فرقی نمیکند که در حال سقوط است یا رشد، پس طبق این ایده، Grid با استفاده از سیستم سفارش باز هوشمند، سفارشات را باز میکند تا در مجموع، این سفارشات در برخی از نقاط، سود کافی کسب کنند تا همه آنها را به یک باره معامله کند. بگذارید این را در تصاویر زیر نشان دهم:
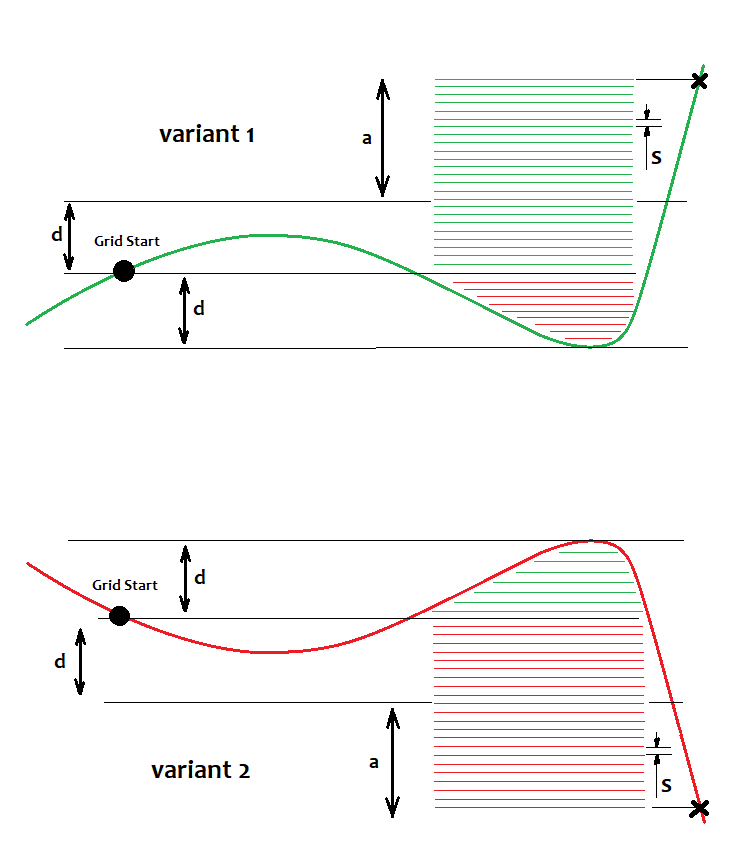
در اینجا من به ترتیب دو گزینه را برای صعود و نزول بازارها نشان داده ام. طبق استراتژی grid، بدون توجه به گزینه ای که انتخاب میکنیم، باید پیروز شویم. کسانی که از سیستم معاملاتی grid استفاده میکنند همیشه میگویند که از سفارشات در حال انتظار استفاده میکنند زیرا با بهترین قیمت راه اندازی میشوند. این درست است، اما من معتقدم که سفارشات بازار، فقط به این دلیل که در زمان ورود، قادر به کنترل spread ها و slippagesها هستید، بدتر نیستند. علاوه بر این، میتوانید ورود را کمی به تعویق بیندازید. با این حال، سفارشات محدود در این استراتژی بهتر است. ما یک نقطه شروع داریم که نسبت به آن سفارشات داده میشود. بالاتر از این نقطه، سفارشات خرید را با مرحله ” s” تنظیم میکنیم، در حالی که در زیر آن، سفارشات فروش را تنظیم میکنیم. اگر قیمت، به آنها برسد، به بازار تبدیل میشوند. این تصویر براساس شرایط خاص قیمت گذاری، سفارشات ثبت شده را نمایش میدهد. نمایش سفارشات محدود در اینجا هیچ فایده ای ندارد زیرا آنها در مدت نامحدودی در یک سطح، بالا و پایین میروند. فقط سفارشات ثبت شده واقعی برای ما مهم هستند زیرا سود یا زیان آنها به ترتیب به مجموع سود یا زیان اضافه میشود. برای اطمینان از سود، برخی سفارشات باید در زمان ” k” بیشتر از بقیه باشد، به عنوان مثال ما باید K = a / d را ارائه دهیم، جایی که K> = K0. با رسیدن به К0، مجموع سود تمام سفارشات grid از آستانه صفر فراتر میرود. ما میتوانیم سود فعلی یک موقعیت یا سفارشات را در مورد MetaTrader 4 به همان روش ساده نیز محاسبه کنیم. به عبارت دیگر، وقتی وضعیت، به سرعت در یک جهت خاص حرکت میکند و پس از حرکت “n ” به سمت بالا یا پایین، سود را به دست میآوریم. به طور دقیق، این نسبت، قابل محاسبه است اما میتوان به راحتی به طور دستی آن را انتخاب کرد. محاسبه احتمالی به شرح زیر است:
- Nl=d/s – 1
- NP=(a+d)/s -1
- Pr=Sum(1,NP)(s*i)=(s+s*NP)*Np/2
- Ls=Sum(1,Nl)(s*j+ s*NP)=(s+s*Nl)*Nl/2+s*NP^2
با جمع کردن ضرر یا سود تمام سفارشات، میتوان دریافت که این مبالغ،به صورت تصاعد حسابی هستند. یک معادله وجود دارد که مجموع تصاعد حسابی را توصیف میکند (با استفاده از اولین و آخرین عبارات آن)، که در اینجا اعمال میشود.
با در نظر گرفتن Pr-Ls = 0 ، حل این معادله، “” a را به دست میدهد که محاسبه K0 = a / d را امکان پذیر میکند. علاوه بر این، استفاده از این معادلات، امکان تعیین ضریب سود و بازده پیشبینی شده چرخه های معاملاتی را که باید موقعیت های باز خرید و فروش را داشته باشند، فراهم میکند.
- Prf=Pr/Ls
- M=(Pr-Ls)/(Np+Nl)
این معادلات به جای کل نمودار، ضریب سود و بازده مورد انتظار یک چرخه معاملاتی خاص را محاسبه میکنند. به شرطی که نمودار ما در نقطه پایان چرخه به پایان برسد، ضریب سود مثبت خواهد بود. چرخه یک grid، جداگانه است. grid ساخته میشود، تا حد ممکن استفاده میشود، موقعیت ها بسته میشوند و grid جدید ساخته میشود. در صورت سپرده بی نهایت، این یک فرآیند بی نهایت است. اینطور است که تقریباً به نظر میرسد روی منحنی است:
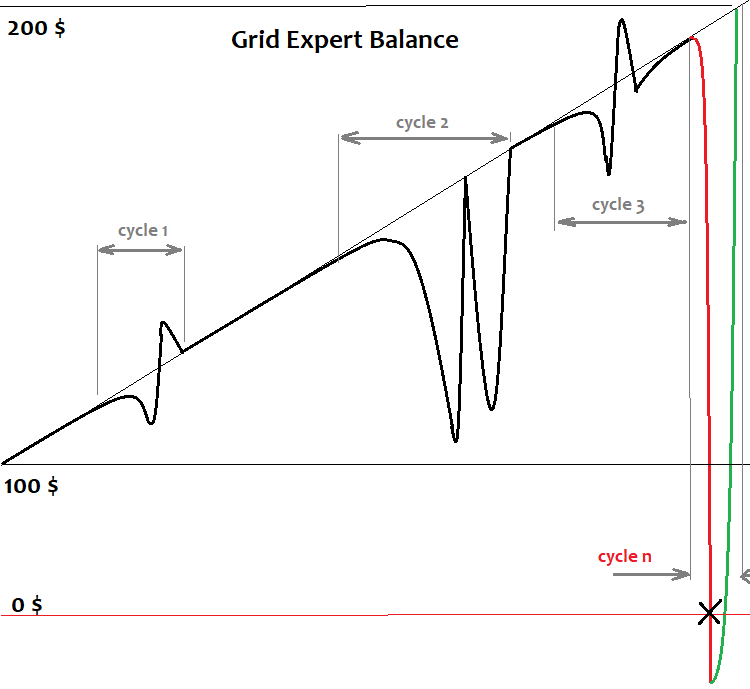
در اینجا من یک نمایش ساده از نمودار تعادل ربات grid هنگام اجرا در گذشته ارائه داده ام. چند چرخه وجود دارد که سپرده، قادر به مقاومت در برابر آنها است و نمودار، بالا میرود. اما این امر، ناگزیر با چرخه ای پایان مییابد که سپرده، کافی نباشد و تمام سود قابل مشاهده ما به دست کارگزار باشد. از نظر ریاضی، این یک چرخه ناتمام محسوب میشود. چرخه ناتمام همیشه بی فایده است و ضرر آن با تمام سودهای کسب شده طی چرخه هایی که تا آخر کار کردهاند همپوشانی دارد. همچنین چرخه ممکن است به دلیل ناکافی بودن سفارشات لازم برای ادامه grid، ناتمام باشد. همه کارگزاران، محدودیت هایی را در تعداد سفارشاتی که به طور همزمان در ترمینال یا یک جفت خاص ثبت شدهاند اعمال میکنند. grid را نمیتوان به طور نامحدود ساخت. حتی اگر فرض کنیم که توانایی انجام چنین کاری را داریم، باز هم در نهایت نتیجه فوق را خواهیم گرفت. در انتهای مقاله، من به طور خلاصه توضیح میدهم که چرا این اتفاق از نظر ریاضی رخ میدهد.
سیستم معاملاتی Martingale و معادلات اساسی آن
مانند grid، ایده پشت martingale پیروزی بدون در نظر گرفتن جهت بازار است. این مبتنی بر همان توهم سود مطلق است. اگر سفارشی را باز کنیم و سودآور به نظر برسد، به سادگی معامله بیشتری میکنیم. به محض ضرر، تعداد سفارش های بعدی ” n” را نسبت به موقعیت از دست رفته افزایش میدهیم. اگر سفارش ما سودآور است، ما به راحتی آن را میبندیم و نسبت به مقدار اولیه، سود بیشتری به دست میآوریم. اگر معلوم شد که بازهم ضرر میکنید، مرحله قبلی را دوباره تکرار کنید در حالی که lot را “n ” بار، نسبت به مجموع بسیاری از موقعیت های از دست رفته درون چرخه افزایش دهید. این کار را تکرار کنید تا دوباره معامله سودآوری داشته باشید. آخرین معامله در این چرخه همیشه سودآور است و سود آن همیشه ضرر معاملات از دست رفته را پوشش میدهد. نمودار به این ترتیب شروع میشود که از چرخه تشکیل شده است. به شرطی که نمودار با آخرین چرخه به پایان برسد، یک انتظار مثبت و ضریب سود به دست میآوریم. مهم نیست که چگونه و کجا این سفارشات را باز میکنیم. ترجیحاً، این سفارشات باید سود و زیان ثابت داشته باشند یا به سادگی در stop level ثابت بسته شوند. در اینجا نشان داده شده است که نمودار تعادل ربات martingale به نظر میرسد:
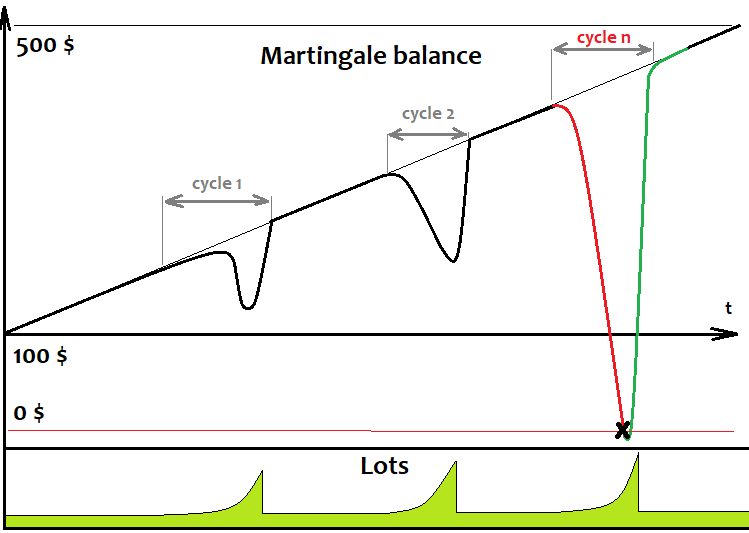
همانطور که میبینیم، از آنجا که martingale به صورت چرخه ای کار میکند، بسیار شبیه grid است، این نمودار کاملاً شبیه نمودار تعادل grid است. تنها تفاوت این است که همیشه یک سفارش واحد را باز میکند و منتظر میماند تا بسته شود تا سفارش بعدی ثبت شود. درست مانند مورد grid، دیر یا زود، سپرده برای اتمام چرخه کافی نیست، تمام سفارشات بسته شده و سپرده از بین میرود. برای اطمینان از چرخه های سودآور، سود آخرین معامله باید ضرر معاملات قبلی را پوشش دهد:
- Nl
- Np=1
- Pr=L[Nl+Np]*TP[Nl+Np]*TickSize
- Ls=Sum(1,Nl)(L[i]*SL[i])*TickSize
در اینجا سود، بیشتر از اینکه بر اساس امتیازات شما محاسبه شود، بر اساس واحد پول حساب شما محاسبه میشود، زیرا سیستم با معاملات بزرگ سروکار دارد. تعداد زیادی سفارش خاص با استفاده از بازگشتی محاسبه میشود:
- L[1]=StartLot
- for(2,Nl) L[i]=(K*Sum(1,i-1)(L[j]*SL[j]))/TP[i]
که در آن ” k” ضریب سود مورد نیاز چرخه است. Spreadهای commissions و swaps در اینجا در نظر گرفته نشده است اما من فکر نمیکنم این مهم باشد. در صورت نیاز، معادلات میتوانند به راحتی اصلاح شوند، اگرچه من نکته ای را در آن نمیبینم. معادلات martingale مشابه معادلات grid هستند. SL و TP ضرر به دست آمده و سود مطلوب یک سفارش هستند. ما می توانیم با حل معادله ساده زیر تعریف را به دست آوریم:
K = (L [i] * TP [i]) / Sum (1، i-1) (L [j] * SL [j]).
توسعه سیستم معاملاتی و آزمایش ساده ترین grid EA
برای آزمایش مفروضات بالا، بیایید یک grid EA ساده و یک martingale ساده به زبان MQL5 بنویسیم تا آنها را آزمایش کرده و نتایج را ببینیم. من قصد دارم با grid شروع کنم. ابتدا چند کلاس مناسب برای کار با موقعیت به الگوی ما اضافه کنید:
#include <Trade\PositionInfo.mqh> #include <Trade\Trade.mqh> CPositionInfo m_position=CPositionInfo();// trade position object CTrade m_trade=CTrade(); // trading object
این دو کتابخانه به طور پیش فرض همیشه در MetaTrader 5 وجود دارد، بنابراین هیچ مشکلی در زمینه تدوین وجود نخواهد داشت.
بعد، بیایید تمام ورودی های لازم را توصیف کنیم:
///grid variables input int MaxChannelSizePoints=500;//Max Of a+d input int MinMoveToClose=100;//Mininum Move input int GridStepPoints=20;//Grid Step In Points input int BarsI=999;//Bars To Start Calculate input double KClose=3.5;//Asymmetry /// ////////minimum trading implementation input int SlippageMaxOpen=15; //Slippage For Open In Points input double Lot=0.01;//Lot input int MagicC=679034;//Magic /////////
بلوک اول تمام پارامترهای grid لازم را پیاده سازی میکند، در حالی که بلوک دوم توانایی معامله یک lot ثابت را در ساده ترین شکل خود اعمال میکند.
هنگام راه اندازی EA، درصورت خاتمه یافتن اشتباه عملکرد، نیاز به تایید و بازیابی پارامترهای grid از جلسه قبلی خواهیم داشت. این ویژگی اختیاری است اما بهتر است قبلاً چنین مواردی را پیاده سازی کنید:
void DimensionAllMQL5Values()////////////////////////////// { ArrayResize(Time,BarsI,0); ArrayResize(High,BarsI,0); ArrayResize(Low,BarsI,0);} void CalcAllMQL5Values()/////////////////////////////////// { ArraySetAsSeries(High,false); ArraySetAsSeries(Low,false); ArraySetAsSeries(Time,false); CopyHigh(_Symbol,_Period,0,BarsI,High); CopyLow(_Symbol,_Period,0,BarsI,Low); CopyTime(_Symbol,_Period,0,BarsI,Time); ArraySetAsSeries(High,true); ArraySetAsSeries(Low,true); ArraySetAsSeries(Time,true); }
این کد برای اجرای آرایه های از پیش تعریف شده برای تکمیل تحلیل اولیه لازم است. بعداً نیازی به این آرایه ها نخواهیم داشت. ما فقط در هنگام محاسبه اولیه از آنها استفاده خواهیم کرد.
بازیابی به روش زیر انجام میشود:
void RestoreGrid()//recover the grid if the robot is restarted {DimensionAllMQL5Values(); CalcAllMQL5Values(); bool ord=PositionSelect(Symbol()); if ( ord && int(PositionGetInteger(POSITION_MAGIC)) == MagicC )} { GridStartTime=datetime(PositionGetInteger(POSITION_TIME)); GridStartPrice=double(PositionGetDouble(POSITION_PRICE_OPEN)); GridUpPrice=GridStartPrice; GridDownPrice=GridStartPrice; for(int i=0;i<BarsI;i++) { if ( High[i] > GridUpPrice ) GridUpPrice=High[i]; if ( Low[i] < GridDownPrice ) GridDownPrice=Low[i]; if ( Time[i] < GridStartTime ) break; } bCanUpdate=true; bTryedAlready=false;
برای ردیابی وضعیت فعلی grid، ما باید متغیرهای دیگری را نشان دهیم که قیمت های بالا و پایین را در طول grid موجود و همچنین قیمت و زمان شروع grid که روی آن تنظیم شده را نشان میدهند.
datetime GridStartTime;//grid construction time double GridStartPrice;//grid starting price double GridUpPrice;//upper price within the corridor double GridDownPrice;//lower price within the corridor
ما همچنین برای ردیابی یا به روزرسانی متغیرهای grid در حین حرکت قیمت و همچنین برای تلاش های اضافی برای بستن grid در صورت عدم موفقیت اولین تلاش، به دو متغیر boolean نیاز داریم.
bool bCanUpdate;//whether it is possible to update the grid bool bTryedAlready;//whether there was an attempt to close a position
ایجاد و به روزرسانی پارامترهای grid در طول توسعه به شرح زیر است:
void CreateNewGrid()//create a new grid { SymbolInfoTick(Symbol(),LastTick); GridStartTime=TimeCurrent(); GridStartPrice=LastTick.bid; GridUpPrice=GridStartPrice; GridDownPrice=GridStartPrice; double SummUp=LastTick.ask+double(GridStepPoints)*_Point; double SummDown=LastTick.bid-double(GridStepPoints)*_Point; while ( SummUp <= LastTick.ask+double(MaxChannelSizePoints)*_Point ) { m_trade.BuyStop(Lot,SummUp,Symbol()); SummUp+=double(GridStepPoints)*_Point;} while ( SummDown >= LastTick.bid-double(MaxChannelSizePoints)*_Point ) {m_trade.SellStop(Lot,SummDown,Symbol()); SummDown-=double(GridStepPoints)*_Point;} void UpdateGrid()//update the grid parameters} { SymbolInfoTick(Symbol(),LastTick); if ( LastTick.bid > GridUpPrice ) GridUpPrice=LastTick.bid; if ( LastTick.bid < GridDownPrice ) GridDownPrice=LastTick.bid;
این توابع برای بستن موقعیت ها و پاکسازی سفارشات محدود باقیمانده و همچنین تابع محمول که شرایط بسته شدن grid را تشخیص میدهد، است:
void ClosePosition()//close a position by a symbol { bool ord; ord=PositionSelect(Symbol()); if ( ord && int(PositionGetInteger(POSITION_MAGIC)) == MagicC )} {if(m_position.SelectByIndex(0)) m_trade.PositionClose(m_position.Ticket());} {void CleanLimitOrders()//clear limit orders} { int orders=OrdersTotal(); for(int i=0;i<orders;i++)} { ulong ticket=OrderGetTicket(i); if(ticket!=0)} {m_trade.OrderDelete(ticket);} bool bCanClose()//closure condition { if ( GridStartPrice == GridUpPrice && (GridStartPrice-GridDownPrice)/_Point >= MinMoveToClose ) return true; if ( GridStartPrice == GridDownPrice && (GridUpPrice-GridStartPrice)/_Point >= MinMoveToClose ) return true; if ( GridStartPrice != GridUpPrice && GridStartPrice != GridDownPrice && (GridStartPrice-GridDownPrice)/(GridUpPrice-GridStartPrice) >= KClose && (GridStartPrice-GridDownPrice)/_Point >= MinMoveToClose ) return true; if ( GridStartPrice != GridDownPrice && GridStartPrice != GridUpPrice && (GridUpPrice-GridStartPrice)/(GridStartPrice-GridDownPrice) >= KClose && (GridUpPrice-GridStartPrice)/_Point >= MinMoveToClose ) return true; /* if ( GridUpPrice >= GridStartPrice+MaxChannelSizePoints*_Point //|| GridDownPrice <= GridStartPrice-MaxChannelSizePoints*_Point ) return true; */ return false;}
من آخرین شرط را در تابع احتمالی توضیح داده ام. در صورت حرکت قیمت به خارج از grid، grid را میبندد. به دلخواه میتوانید از آن استفاده کنید، هیچ چیز دیگری تغییر نمیکند. اکنون فقط باید تابع معامله اصلی را بنویسیم:
void Trade()//the main function where all actions are performed { bool ord=PositionSelect(Symbol()); if ( bCanUpdate ) UpdateGrid(); if ( ord && bCanClose() )//if there is a position and the closing condition is met { ClosePosition(); CleanLimitOrders(); bCanUpdate=false; bTryedAlready=true;} if ( bTryedAlready ) ClosePosition(); if ( !bCanUpdate && !ord ) { CleanLimitOrders(); CreateNewGrid(); bCanUpdate=true; bTryedAlready=false;} }
همچنین، بیایید تعریف کنیم که هنگام مقداردهی اولیه کجا و چه چیزی فراخوانی شود و چه کاری انجام شود:
int OnInit() { m_trade.SetExpertMagicNumber(MagicC);//set the magic number for positions RestoreGrid();//restore the grid if present return(INIT_SUCCEEDED); } void OnTick() { Trade(); }
ما grid EA را توسعه داده ایم. حالا بیایید آن را تست کنیم و ببینیم چگونه رفتار میکند:
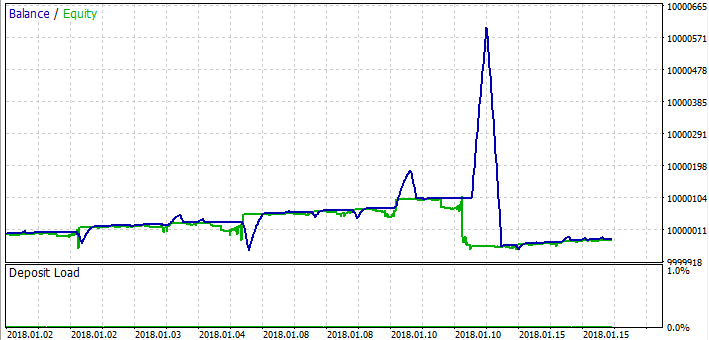
همانطور که میبینید، فرضیات مربوط به چرخه بیسود تایید شده است. در ابتدا، grid بسیار خوب کار میکند، اما بعد، لحظه ای فرا میرسد که grid کافی نیست و منجر به از دست دادن یک چرخه میشود و تمام سود را از بین میبرد. بخشهای مرسوم روند بازار معمولاً نتایج خوبی را نشان میدهند، در حالی که بیشتر ضررها در بخشهای flat رخ میدهد. نتیجه کلی همیشه ضرر است زیرا هنوز هم spread داریم.
توسعه و آزمایش ساده ترین martingale EA
اکنون که به grid پرداختیم، بیایید به سراغ martingale EA برویم. کد آن بسیار ساده تر خواهد بود. برای کار با موقعیت ها، از کتابخانه های اعمال شده در grid EA استفاده خواهیم کرد. نمایش کد برای بار دوم فایده ای ندارد. بیایید ورودی ها را بلافاصله در نظر بگیریم:
input int SLE=100;//Stop Loss Points input int TPE=300;//Take Profit Points input int SlippageMaxOpen=15; //Slippage For Open In Points input double Lot=0.01;//Start Lot input int MagicC=679034;//Magic input int HistoryDaysLoadI=10;//History Deals Window Days
برای سادگی بیشتر، من سیستمی را انتخاب کرده ام که در آن موقعیت ها کاملاً با حد ضرر بسته میشوند یا سود میبرند. آخرین متغیر به ما اجازه میدهد تا از بارگذاری پیوسته کل تاریخ سفارش جلوگیری کنیم، در عوض فقط از پنجره لازم (فقط برای بهینه سازی) استفاده کنیم. به اعتقاد من، سایر متغیرها بدیهی هستند.
EA به طور برجسته فقط دو تابع دارد:
double CalcLot()//calculate the lot { bool ord; double TotalLot=0; HistorySelect(TimeCurrent()-HistoryDaysLoadI*86400,TimeCurrent()); for ( int i=HistoryDealsTotal()-1; i>=0; i-- ) { ulong ticket=HistoryDealGetTicket(i); ord=HistoryDealSelect(ticket); if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT ) { if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) < 0 ) { TotalLot+=HistoryDealGetDouble(ticket,DEAL_VOLUME); } else { break; } } } return TotalLot == 0 ? Lot: TotalLot; } void Trade()//the main function where all actions are performed { bool ord=PositionSelect(Symbol()); SymbolInfoTick(Symbol(),LastTick); if ( !ord ) { if ( MathRand() > 32767.0/2.0 ) { m_trade.Buy(CalcLot(),_Symbol,LastTick.ask,LastTick.bid-double(SLE)*_Point,LastTick.ask+double(TPE)*_Point); } else { m_trade.Sell(CalcLot(),_Symbol,LastTick.ask,LastTick.ask+double(SLE)*_Point,LastTick.bid-double(TPE)*_Point); } } }
اولین مورد، برای محاسبه lot نهایی استفاده شده برای باز کردن یک موقعیت پس از بررسی سوابق معامله مورد نیاز است. اگر آخرین معامله بی سود باشد، قرعه بعدی برابر است با مجموع بسیاری از معاملات باخت قبلی تا معامله سودآور اول. اگر آخرین معامله سودآور است، مقدار lot را به مقدار اولیه خود تنظیم کنید. در تابع اصلی، ما سفارشات را در جهات مختلف با stop level ثابت به طور تصادفی باز میکنیم، در حالی که حجم معاملات با استفاده از تابع اول محاسبه میشوند. برای اینکه همه اینها به درستی کار کنند، باید یک مقدار خارق العاده به EA در مقداردهی اولیه اختصاص دهیم، در حالی که تابع اصلی همانند grid در handler OnTick فراخوانی میشود.
این نتیجه گیری از توسعه ساده ترین سیستم معاملاتی martingale است. حالا بیایید آن را تست کنیم و نتیجه را ببینیم:
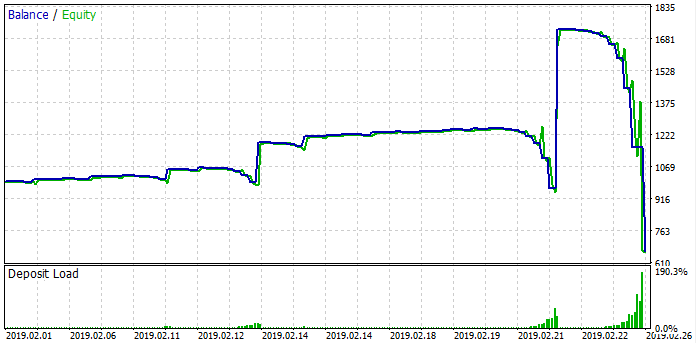
این مورد مشابه grid است. ما میتوانیم چرخه ها را ببینیم. martingale EA تا قبل از شروع چرخه زیان درست کار میکند. margin برای معامله باز بعدی کافی نیست و ضرر اتفاق میافتد. درست مثل grid، بعضی جاها کار میکند، و بعضی جاها نه، اما همیشه به ضرر ختم میشود. اکنون که هر دو استراتژی را مورد بررسی قرار دادیم، زمان آن رسیده است که نتیجه گیری ریاضی کنیم و ما را به پاسخ های مهم تری از درک این دو استراتژی سوق دهد.
ریاضیات رایج پشت grid و martingale
چرا معتقدم ریاضیات رایج پشت grid و martingale بسیار مهم است؟ اگر آن را کاملاً درک کنیم، میتوانیم سرانجام از یک سری ایده هایی که هرگز برای ما سودآوری نخواهد داشت خداحافظی کنیم، اگرچه ممکن است بخواهیم به آنها باور داشته باشیم. حداقل، ما خواهیم فهمید که چه شرایطی میتواند در عملکرد این استراتژی ها نقش داشته باشد. علاوه بر این، ما متوجه خواهیم شد که چرا martingale pure و grid استراتژی های خود را از دست می دهند.
بیایید تصور کنیم که هر استراتژی از تعداد بی نهایت استراتژیهای بسیار ساده تشکیل شده است. وقتی سفارشی باز میشود، یکی از آنها فعال میشود. ما فرض خواهیم کرد که این سفارشات با ضرر یا سود ثابت بسته میشوند. بیایید آنها را با آرایههای C [i] و Lot [i] مطابقت دهیم که اندازه این آرایه ها برابر است و به بی نهایت متمایل است. فرض کنید lot اعمال شده توسط هر یک از استراتژی ها همیشه متفاوت باشد. همچنین، بیایید احتمال ایجاد هر یک از این استراتژی ها را معرفی کنیم. البته PC [i]، رویدادهای یک گروه کامل را تشکیل میدهند به طوری که Sum(0,n) ، (PC [i] = 1). همه نتایج این رویدادها فضاهای رویداد جدید S [i] ، T [i] را تشکیل میدهند که به ترتیب فعالیتهای ضرر و سود را نشان میدهد. این رویدادها، احتمالات شرطی PS [i] ، PT [i] خود را دارند که البته گروه کاملی نیز تشکیل میدهند. نمایش گرافیکی در زیر ارائه شده است:
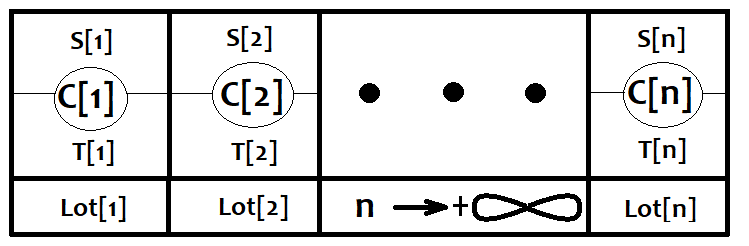
حال بیایید هر استراتژی واحدی را از این لیست در نظر بگیریم و بازده مورد انتظار آن را محاسبه کنیم:
M[i]=(PT[i]*TP-PS[i]*SL)*Lot[i]*TickSize.
اگر از جهت قیمت در نقاط باز شدن معامله اطلاع نداشته باشیم، می توان گفت که M [i] = 0، به طوری که M [i] آرایه ای از بازده مورد انتظار استراتژی های مشخص است. به عبارت دیگر، اگر ما ندانیم که قیمت به کجا میرود، بدون توجه به نحوه معامله، 0 میگیریم به شرطی که تعداد معاملات به بی نهایت متمایل باشد.
معادله کلی بازده مورد انتظار به صورت زیر است:
M0=Sum(0,n)(PC[i]*M[i])
ما میدانیم که وقتی n به سمت بی نهایت تمایل دارد، همه M [i] به صفر میرسد، به این معنی که تمام شرایط حاصل از جمع ما به 0 گرایش دارند در حالی که تعداد استراتژی ها محدود است و تعداد معاملات بی نهایت است. این، به نوبه خود، به این معنی است که بازده کلی مورد انتظار M0 هنوز برابر 0 است. اگر بیشتر فکر کنیم، معلوم میشود که یک مجموعه نامحدود از چنین مجموعه های محدودی از استراتژی ها نیز برابر با صفر است، زیرا خلاصه کردن تعداد بی نهایت صفر نتیجه 0 میدهد. در مورد grid ، اندازه lot در همه جا یکسان است، در حالی که در مورد martingale، متفاوت است، اما این تفاوت به هیچ وجه بر انتظار نهایی تاثیر نمیگذارد. هر دو استراتژی را میتوان با استفاده از این معادله عمومی توصیف کرد بدون اینکه حتی در مورد ترکیبیات زحمت بکشید. همه چیز کاملاً ساده و سرراست است.از آنجا که میتوان این استراتژی ها را با استفاده از این معادله توصیف کرد، پس برای هر استراتژی مفید است. این نتیجه گیری این است که همه استراتژی های شامل تغییر و دستکاری حجم معاملات، و همچنین سیستم های باز/بسته سفارش از هر پیچیدگی بدون دانستن جهت حرکت تقریبی در زمان باز و بسته شدن معاملات یا حداقل برخی از پارامترهای بازار کمکی محکوم به شکست هستند. بدون پیش بینی صحیح، تمام تلاشهای ما صرفاً اتلاف وقت و هزینه است.
نحوه استفاده صحیح ازسیستم معاملاتی grid و martingale
در صورت اطلاع از حرکت آینده بازار در جهتی خاص یا احتمال بالای وقوع چنین رویدادی، grid ممکن است مفید باشد، در حالی که خطر ایجاد gap نیز وجود دارد. Gapها و gridها خیلی خوب با هم ترکیب نمیشوند. این به این دلیل است که سفارشات در مرحله مشخص قرار میگیرند و ممکن است این اتفاق بیفتد که تیک بعدی از کنار همه سفارشات عبور کند و بسیار فراتر از grid ظاهر شود. البته، این یک موقعیت نادر است، اما به طور حتم کارایی سیستم را کاهش میدهد. اندازه grid باید مساوی یا کمی کمتر از حرکت پیش بینی شده تنظیم شود، در حالی که نیازی به دانستن جهت حرکت نیست، بلکه فقط مقدار تقریبی آن را بدانید کافی است. در زیر نحوه مشاهده نمودار تعادل در صورت موفقیت آمیز بودن الگوریتم تشخیص trend نشان داده شده است:
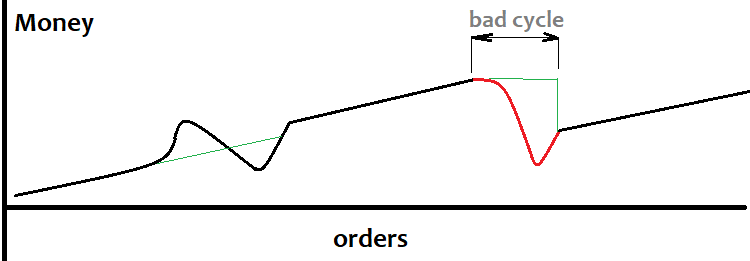
همیشه امکان تعیین trend از قبل وجود ندارد. این اغلب منجر به از دست دادن چرخه میشود (که در بالا با رنگ قرمز مشخص شده است) و کشش آن نیز بسیار زیاد است. سیستم معاملاتی grid ممکن است برای کسانی که روشهای تشخیص حرکات بزرگ را دارند مفید باشد. در این حالت، grid میتواند براساس سیگنال سفارشی تنظیم شود. من هنوز به این سوال نپرداختهام، بنابراین اگر کسی الگوریتم های خوبی برای تشخیص حرکات بزرگ دارد، در صورت تمایل، تجربه خود را به اشتراک بگذارید.
حالا بیایید،سیستم معاملاتی martingale را در نظر بگیریم. اگر سیگنالی با بازده مورد انتظار “0” داشته باشیم، اما میدانیم که دنباله ضررها به حدی است که احتمال یک معامله سودآور برای تعداد معینی از ضررها در یک ردیف نزدیک به یک است، پس سیگنال میتواند برای martingale استفاده شود نمودار تعادل به این شکل است:
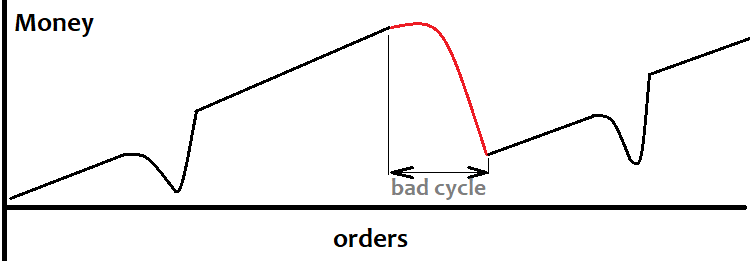
اما من شخصاً اعتقاد دارم که سیستم معاملاتی martingale در هر صورت خطرناک است. من معتقدم دستیابی به چنین شرایطی که توصیف کردم تقریباً غیرممکن است، اگرچه در مورد سیستم معاملاتی grid همه چیز به نظر آسانتر و از همه مهم تر واضح تر است.
نتیجه گیری
در این مقاله، در رابطه با سیستم معاملاتی سعی کردم این دو استراتژی (martingale،grid) را تا حد امکان با تشریح شباهت ها، مزایا و معایب آنها شرح دهم. من معتقدم، درک همه توضیحات حتی برای مبتدیان نیز آسان است. این مقاله بیشتر برای معامله گران تازه کار در نظر گرفته شده است، با این حال نتیجه گیریهای حاصل از آن بسیار مهمتر از ارزیابی ساده استراتژی ها و محدودیت های کاربرد آنها است. نتیجه گیری های کلی ریاضی که در اینجا ارائه میشود به همه این امکان را میدهد تا ضمن توسعه سیستم های معاملاتی خود، از وقت خود به نحو احسن استفاده کنند. این مقاله برای درک فیزیک بازار چیز جدیدی در پی ندارد، اما من فکر میکنم این میتواند از بسیاری از معامله گران جلوگیری کند تا از این اصول برای منافع خود استفاده نکنند.
این مقاله ترجمه شده توسط تیم آکادمی ایران ام کیو ال می باشد.





پاسخها
سلام
من خدایی چیزی نفهمیدم
ای کاش این مقاله را برروی یک فایل تصویری مانند یک فیلم توضیح می دادید. تشکر
بله متاسفانه ترجمه به درستی انجام نشده ،در برنامه هام این نوع اموزش رو قرار خواهم داد
سلام
در خصوص استراتژی های مارتینگل، گرید و … خیلی کار کردم، اگر مایل بودین زمانی رو معین کنین که با هم به تبادل نظر بپردازیم.
سلام؛حتما یه پیام در صفحه تماس با ما بگذارید تا بتونم بهتون ایمیل بزنم
بسیار جالب و مفید بود .تشکر فراوان از شما استاد ارجمند.